प्रतिपादक नियम

प्रतिपादक नियम, प्रतिपादक के नियम और उदाहरण।

• एक घातांक क्या है
• खर्च के नियम
• खर्च करने वाला कैलकुलेटर

एक घातांक क्या है

N की शक्ति के लिए उठाया गया आधार, n, गुणा के गुणा के बराबर है:

a ⁿ = a × a × ... × a

                    n बार

a आधार है और n घातांक है।

उदाहरण

३ ^१ = ३

3 ² = 3 × 3 = 9

3 ³ = 3 × 3 × 3 = 27

3 ⁴ = 3 × 3 × 3 × 3 = 81

3 ⁵ = 3 × 3 × 3 × 3 × 3 = 243

व्यय नियम और गुण

नियम का नाम	नियम	उदाहरण
उत्पाद नियम	एक n ⋅ एक मीटर = एक n + m	2 3। 2 4 = 2 3 + 4 = 128
	एक n ⋅ ख n = ( एक ⋅ ख ) n	3 2 = 4 2 = (3⋅4) 2 = 144
भाववाचक नियम	a n / a m = a n - m है	2 5 /2 3 = 2 5-3 = 4
	a n / b n = ( a / b ) n	4 3 /2 3 = (4/2) 3 = 8
शक्ति नियम	( b n ) m = b n⋅m	(२ ३ ) २ = २ ३⋅२ = ६४
	b n m = b ( n m )	2 3 2 = 2 ( 3 2 ) = 512
	m m ( b n ) = b n / m	2 2 (2 6 ) = 2 6/2 = 8
	ख 1 / n = n √ ख	8 1/3 = 3 √ 8 = 2
नकारात्मक घातांक	b -n = 1 / b n	2 -3 = 1/2 3 = 0.125
शून्य नियम	बी ० = १	५ ० = १
	0 एन = 0, एन / 0 के लिए	० ५ = ०
एक नियम	बी 1 = बी	५ १ = ५
	1 एन = 1	१ ५ = १
माइनस एक नियम		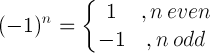(-1) 5 = -1
व्युत्पन्न नियम	( एक्स एन ) ' = n ⋅ एक्स एन -1	( x 3 ) ' = 3⋅ x 3-1
एकात्म शासन	∫ x n dx = x n +1 / ( n +1) + C	∫ x 2 dx = x 2 + 1 / (2 + 1) + C

उत्पाद नियम के प्रतिपादक

उसी आधार के साथ उत्पाद नियम

एक ⁿ ⋅ एक ^मीटर = एक ^{n + m}

उदाहरण:

2 ^{3 7} 2 ⁴ = 2 ^{3 + 4} = 2 ⁷ = 2⋅2⋅2⋅2⋅2⋅2⋅2⋅2 = 128

समान प्रतिपादक के साथ उत्पाद नियम

एक ⁿ ⋅ ख ⁿ = ( एक ⋅ ख ) ⁿ

उदाहरण:

3 ² = 4 ² = (3⋅4) ² = 12 ² = 12 =12 = 144

देखें: घातांक बढ़ाना

घातांक के नियम

एक ही आधार के साथ कोटेटिव नियम

a ⁿ / a ^m = a ^{n - m है}

उदाहरण:

2 ⁵ /2 ³ = 2 ^5-3 = 2 ² = 2⋅2 = 4

एक ही प्रतिपादक के साथ भावुक नियम

a ⁿ / b ⁿ = ( a / b ) ⁿ

उदाहरण:

4 ³ /2 ³ = (4/2) ³ = 2 ³ = 2⋅2⋅2 = 8

देखें: घातांक का विस्तार

ययय यययययय यययय यययय यययय यययय यययय यययय यययय यययय यययय यययय यययय यययय यययय ययययय यययययय ययययय यययय यययय यययय यययययय यययय यययय यययय ययययययय ययययययय यययययययययययययययययययययययय यययय ययय ययययययय))

सत्ता शासन मैं

( a ⁿ ) ^m = a ^n⋅m

उदाहरण:

(2 ³ ) ² = 2 ^3⋅2 = 2 ⁶ = 2⋅2⋅2⋅2⋅2⋅2 = 64

शक्ति नियम II

_एक n ^मीटर _{= एक} ( एन ^एम )

उदाहरण:

₂ 3 ² _{= 2} (3 ² ) _{= 2} (3⋅3) _{= 2} 9 _{= 2⋅2⋅2⋅2⋅2⋅2⋅2⋅2⋅2 = 512}

कट्टरपंथी के साथ सत्ता का शासन

^{m m} ( a ⁿ ) = a ^{n / m}

उदाहरण:

^{2 2} (2 ⁶ ) = 2 ^6/2 = 2 ³ = 2⋅2 =2 = 8

नकारात्मक प्रतिपादक नियम

b ^-n = 1 / b ⁿ

उदाहरण:

2 ^-3 = 1/2 ³ = 1 / (2⋅2 )2) = 1/8 = 0.125

देखें: नकारात्मक घातांक

घातांक कैलकुलेटर ►

यह सभी देखें

• घातांे को जोड़ना
• घातांक का विभाजन
• आंशिक विस्तारक
• बहुत से विस्तारक
• नकारात्मक घातांक
• घातांक को सरल बनाना
• शून्य घातांक
• प्रतिपादक कैलकुलेटर
• लघुगणक कैलकुलेटर
• घातीय वृद्धि कैलकुलेटर
• Antilog कैलकुलेटर
• लॉग (x) नियम
• ln (x) नियम
• ई स्थिर