Arccos (x) függvény
Arccos (x), cos -1 (x), inverz koszinusz- függvény.
Arccos definíció
Az x arccosine az x inverz koszinuszfüggvénye , ha -1≤x≤1.
Ha y koszinusa egyenlő x-szel:
cos y = x
Ekkor x arccosine egyenlő az x inverz koszinusz-függvényével, amely megegyezik y-vel:
arccos x = cos -1 x = y
(Itt a cos -1 x az inverz koszinust jelenti, és nem a koszinust jelenti a -1 erejéhez).
Példa
arccos 1 = cos -1 1 = 0 rad = 0 °
Az arccók grafikonja
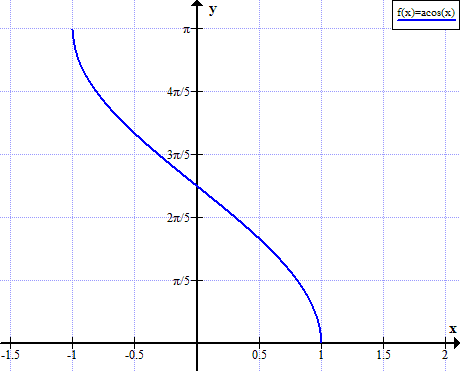
Arccos szabályai
| Szabály neve | Szabály |
|---|---|
| Arkuszin koszinusa | cos (arccos x ) = x |
| Koszinusz-arckozin | arccos (cos x ) = x + 2 k π, amikor k ∈ℤ ( k egész szám) |
| Arccos negatív érv | arccos (- x ) = π - arccos x = 180 ° - arccos x |
| Kiegészítő szögek | arccos x = π / 2 - arcsin x = 90 ° - arcsin x |
| Arccos összeg | arccos ( α ) + arccos ( β ) = arccos ( αβ - √ (1- α 2 ) (1- β 2 ) ) |
| Arccos különbség | arccos ( α ) - arccos ( β ) = arccos ( αβ + √ (1- α 2 ) (1- β 2 ) ) |
| Az x bűnének arccói | arccos (sin x ) = - x - (2 k +0,5) π |
| Szinkron arccosine | |
| Arccosine tangense |  |
| Az arccosine származéka | 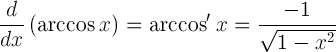 |
| Az arccosine határozatlan integrálja | |
Arccos asztal
| x | arccos (x) (rad) |
arccos (x) (°) |
|---|---|---|
| -1 | π | 180 ° |
| -√ 3 /2 | 5π / 6 | 150 ° |
| -√ 2 /2 | 3π / 4 | 135 ° |
| -1/2 | 2π / 3 | 120 ° |
| 0 | π / 2 | 90 ° |
| 1/2 | π / 3 | 60 ° |
| √ 2 /2 | π / 4 | 45 ° |
| √ 3 /2 | π / 6 | 30 ° |
| 1 | 0 | 0 ° |
Lásd még
- Koszinusz funkció
- Arcsine funkció
- Arctanfunction
- Arccos számológép
- Radián fokban konverter
- Arccos 0
- Arccos of 1
- Arccos of 2
- Arccos of 3
- Arccos of cos
- A bűn arccosai
- Arccos-származék
- Arccos grafikon
- Arccosok
- Az arccosok bűne
- Arccos tan