„Arccos“ (x) funkcija
Arccos (x), cos -1 (x), atvirkštinė kosinuso funkcija.
Arccos apibrėžimas
X arkozinas apibrėžiamas kaip atvirkštinė x kosinuso funkcija, kai -1≤x≤1.
Kai y kosinusas yra lygus x:
cos y = x
Tada x arkozinas yra lygus atvirkštinei x kosinuso funkcijai, kuri lygi y:
arccos x = cos -1 x = y
(Čia cos -1 x reiškia atvirkštinį kosinusą ir nereiškia kosinuso -1 galiai).
Pavyzdys
arccos 1 = cos -1 1 = 0 rad = 0 °
Arccos grafikas
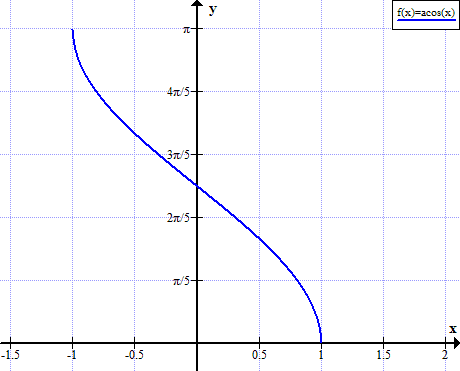
Arccos taisyklės
| Taisyklės pavadinimas | Taisyklė |
|---|---|
| Arkosino kosinusas | cos (arccos x ) = x |
| Kosinuso arkozinas | arccos (cos x ) = x + 2 k π, kai k ∈ℤ ( k yra sveikas skaičius) |
| Neigiamo argumento „Arccos“ | arccos (- x ) = π - arccos x = 180 ° - arccos x |
| Papildomi kampai | arccos x = π / 2 - arcsin x = 90 ° - arcsin x |
| Arccos suma | arccos ( α ) + arccos ( β ) = arccos ( αβ - √ (1- α 2 ) (1- β 2 ) ) |
| Arccos skirtumas | arccos ( α ) - arccos ( β ) = arccos ( αβ + √ (1- α 2 ) (1- β 2 ) ) |
| X nuodėmės arkos | arccos (sin x ) = - x - (2 k +0,5) π |
| Arkosino sinusas | |
| Arkozino tangentas | 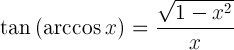 |
| Arkosino darinys | 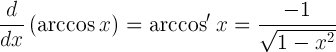 |
| Neapibrėžtas arckozino integralas | |
„Arccos“ stalas
| x | arccos (x) (rad) |
arccos (x) (°) |
|---|---|---|
| -1 | π | 180 ° |
| -√ 3 /2 | 5π / 6 | 150 ° |
| -√ 2 /2 | 3π / 4 | 135 ° |
| -1/2 | 2π / 3 | 120 ° |
| 0 | π / 2 | 90 ° |
| 1/2 | π / 3 | 60 ° |
| √ 2 /2 | π / 4 | 45 ° |
| √ 3 /2 | π / 6 | 30 ° |
| 1 | 0 | 0 ° |
Taip pat žiūrėkite
- Kosinuso funkcija
- Arcsine funkcija
- Arktano funkcija
- „Arccos“ skaičiuoklė
- Radianai į laipsnius konverteris
- 0 „Arccos“
- 1 Arccos
- „Arccos“ iš 2
- „Arccos“ iš 3
- „Arccos of cos“
- Arccos nuodėmės
- Arccos darinys
- „Arccos“ grafikas
- Arccos kos
- Arko nuodėmė
- Arkos įdegis
TRIGONOMETRIJA
- „Arccos“ funkcija
- Arcsino funkcija
- Arktano funkcija
- Kosinuso funkcija
- Sinuso funkcija
- Tangento funkcija