Dabiskais logaritms - ln (x)
Dabiskais logaritms ir skaitļa bāzes e logaritms.
- Dabiskā logaritma (ln) definīcija
- Dabiskā logaritma (ln) likumi un īpašības
- Komplekss logaritms
- Ln (x) grafiks
- Dabisko logaritmu (ln) tabula
- Dabiskā logaritma kalkulators
Dabiskā logaritma definīcija
Kad
e y = x
Tad bāzes x logaritms ir
ln ( x ) = log e ( x ) = y
E konstante vai Eilera numurs ir:
e ≈ 2,71828183
Ln kā eksponenciālās funkcijas apgrieztā funkcija
Dabiskā logaritma funkcija ln (x) ir eksponenciālās funkcijas e x apgrieztā funkcija .
Ja x/ 0,
f ( f -1 ( x )) = e ln ( x ) = x
Vai
f -1 ( f ( x )) = ln ( e x ) = x
Dabiskā logaritma likumi un īpašības
| Kārtulas nosaukums | Noteikums | Piemērs |
|---|---|---|
Produkta noteikums |
ln ( x ∙ y ) = ln ( x ) + ln ( y ) |
ln (3 ∙ 7) = ln (3) + ln (7) |
Quotient likums |
ln ( x / y ) = ln ( x ) - ln ( y ) |
ln (3 / 7) = ln (3) - ln (7) |
Jaudas noteikums |
ln ( x y ) = y ∙ ln ( x ) |
ln (2 8 ) = 8 ∙ ln (2) |
atvasinājums |
f ( x ) = ln ( x ) ⇒ f ' ( x ) = 1 / x | |
neatņemams |
∫ ln ( x ) dx = x ∙ (ln ( x ) - 1) + C | |
Negatīvā skaitļa ln |
ln ( x ) nav definēts, ja x ≤ 0 | |
ln no nulles |
ln (0) nav definēts | |
Viens no tiem |
ln (1) = 0 | |
Bezgalības ln |
lim ln ( x ) = ∞, kad x → ∞ | |
| Eulera identitāte | ln (-1) = i π |
Logaritma produkta noteikums
X un y reizināšanas logaritms ir x logaritma un y logaritma summa.
log b ( x ∙ y ) = log b ( x ) + log b ( y )
Piemēram:
log 10 (3 ∙ 7) = log 10 (3) + log 10 (7)
Logaritma koeficienta noteikums
X un y dalījuma logaritms ir x un y logaritma starpība.
log b ( x / y ) = log b ( x ) - log b ( y )
Piemēram:
log 10 (3 / 7) = log 10 (3) - log 10 (7)
Logaritma jaudas noteikums
X, kas paaugstināts līdz y jaudai, logaritms ir y reizes lielāks par x logaritmu.
log b ( x y ) = y ∙ log b ( x )
Piemēram:
log 10 (2 8 ) = 8 ∙ log 10 (2)
Dabiskā logaritma atvasinājums
Dabiskā logaritma funkcijas atvasinājums ir abpusējā funkcija.
Kad
f ( x ) = ln ( x )
F (x) atvasinājums ir:
f ' ( x ) = 1 / x
Dabiskā logaritma neatņemama sastāvdaļa
Dabiskā logaritma funkcijas integrālu izsaka:
Kad
f ( x ) = ln ( x )
F (x) integrālis ir:
∫ f ( x ) dx = ∫ ln ( x ) dx = x ∙ (ln ( x ) - 1) + C
Ln no 0
Dabiskais nulles logaritms nav noteikts:
ln (0) nav definēts
Kad x tuvojas nullei, x dabiskā logaritma 0 robeža ir mīnus bezgalība:
![]()
Ln no 1
Dabiskais logaritms vienam ir nulle:
ln (1) = 0
Ln bezgalība
Bezgalības dabiskā logaritma robeža, kad x tuvojas bezgalībai, ir vienāds ar bezgalību:
lim ln ( x ) = ∞, kad x → ∞
Komplekss logaritms
Kompleksam skaitlim z:
z = re iθ = x + iy
Kompleksais logaritms būs (n = ...- 2, -1,0,1,2, ...):
Log z = ln ( r ) + i ( θ + 2nπ ) = ln (√ ( x 2 + y 2 )) + i · arctan ( y / x ))
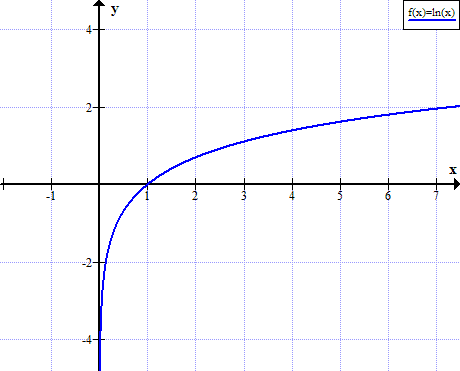
Ln (x) grafiks
ln (x) nav definēts reālām pozitīvām x vērtībām:
Dabisko logaritmu tabula
| x | ln x |
|---|---|
| 0 | nenoteikts |
| 0 + | - ∞ |
| 0,0001 | -9,210340 |
| 0,001 | -6,907755 |
| 0,01 | -4.605170 |
| 0.1 | -2,302585 |
| 1 | 0 |
| 2 | 0.693147 |
| e ≈ 2,7183 | 1 |
| 3 | 1.098612 |
| 4 | 1.386294 |
| 5 | 1.609438 |
| 6 | 1,791759 |
| 7 | 1.945910 |
| 8 | 2.079442 |
| 9 | 2.197225 |
| 10 | 2.302585 |
| 20 | 2.995732 |
| 30 | 3.401197 |
| 40 | 3.688879 |
| 50 | 3.912023 |
| 60 | 4.094345 |
| 70 | 4.248495 |
| 80 | 4.382027 |
| 90 | 4.499810 |
| 100 | 4.605170 |
| 200 | 5.298317 |
| 300 | 5.703782 |
| 400 | 5.991465 |
| 500 | 6.214608 |
| 600 | 6.396930 |
| 700 | 6.551080 |
| 800 | 6.684612 |
| 900 | 6.802395 |
| 1000 | 6.907755 |
| 10000 | 9.210340 |
Skatīt arī
- Logaritms (žurnāls)
- Dabiskā logaritma kalkulators
- Dabiskais nulles logaritms
- Dabiskais logaritms vienā
- Dabiskais logaritms e
- Dabiskais bezgalības logaritms
- Negatīvā skaitļa naturālais logaritms
- Ln apgrieztā funkcija
- ln (x) grafiks
- Dabiskā logaritma tabula
- Logaritma kalkulators
- e nemainīgs
ALGEBRA
ĀTRAS TABULAS