तफावत
संभाव्यता आणि आकडेवारीमध्ये, यादृच्छिक चलचे भिन्नता म्हणजे सरासरी मूल्यापासून चौरस अंतराचे सरासरी मूल्य. हे रॅंडम व्हेरिएबल मधल्या मूल्याजवळ कसे वितरित केले जाते हे दर्शवते. लहान भिन्नता सूचित करते की यादृच्छिक व्हेरिएबल मधल्या मूल्याजवळ वितरित केले जाते. मोठा फरक सूचित करतो की यादृच्छिक व्हेरिएबल मधल्या मूल्यापासून खूपच जास्त वितरित केले जाते. उदाहरणार्थ, सामान्य वितरणासह, अरुंद बेल वक्रात लहान भिन्नता असेल आणि वाइड बेल कर्व्हमध्ये मोठा फरक असेल.
भिन्नता व्याख्या
यादृच्छिक व्हेरिएबल X चे भिन्नता X च्या फरकांच्या वर्गांची अपेक्षित मूल्य आणि अपेक्षित मूल्य μ.
σ 2 = वार ( एक्स ) = ई [( एक्स - μ ) 2 ]
आपल्याला मिळणार्या भिन्नतेच्या परिभाषेतून
σ 2 = वार ( एक्स ) = ई ( एक्स 2 ) - μ 2
सतत यादृच्छिक चलचे भिन्नता
मध्यम मूल्य value आणि संभाव्यता घनता फंक्शन एफ (एक्स) सह सतत यादृच्छिक चल करीता:
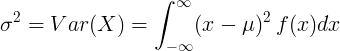
किंवा
![वार (एक्स) = \ डावा [\ अंत _ {- ty इन्फ्टी} ^ {\ इन्फ्टी} x ^ 2 \: एफ (एक्स) डीएक्स \ उजवीकडे] - \ म्यू ^](variance/cont_var2.gif)
वेगळ्या यादृच्छिक चलचे भिन्नता
मध्यम मूल्य with आणि संभाव्यता मास फंक्शन पी (एक्स) सह वेगवान यादृच्छिक चल एक्ससाठी:
![]()
किंवा
![वार (एक्स) = \ डावा [\ योग_ {i} ^ {} x_i ^ 2 पी (x_i) \ उजवा] - \ म्यू ^ 2](variance/disc_var2.gif)
भिन्नतेचे गुणधर्म
जेव्हा एक्स आणि वाई स्वतंत्र यादृच्छिक चल असतात:
वार ( एक्स + वाय ) = वार ( एक्स ) + वार ( वाय )
हे देखील पहा
संभाव्यता आणि सांख्यिकी
वेगवान सारण्या