संभाव्यता वितरण
संभाव्यतेमध्ये आणि आकडेवारीचे वितरण यादृच्छिक व्हेरिएबलचे वैशिष्ट्य आहे, प्रत्येक मूल्यामध्ये यादृच्छिक चलच्या संभाव्यतेचे वर्णन करते.
प्रत्येक वितरणामध्ये विशिष्ट संभाव्यता घनता कार्य आणि संभाव्यता वितरण कार्य असते.
संभाव्य वितरणांची अनिश्चित संख्या असूनही, तेथे अनेक सामान्य वितरण आहेत.
संचयी वितरण कार्य
संभाव्यता वितरण संचयी वितरण कार्य एफ (एक्स) द्वारे वर्णन केले आहे,
x पेक्षा लहान किंवा समान मूल्य मिळविण्यासाठी यादृच्छिक चल X ची संभाव्यता:
फॅ ( एक्स ) = पी ( एक्स ≤ x )
सतत वितरण
संचयी वितरण कार्य एफ (एक्स) ची गणना सतत यादृच्छिक व्हेरिएबल एक्सच्या संभाव्यता घनता फंक्शन एफ (यू) च्या समाकलनाद्वारे केली जाते.
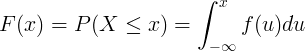
स्वतंत्र वितरण
संचयी वितरण कार्य एफ (एक्स) ची भिन्नता यादृच्छिक व्हेरिएबल एक्स च्या संभाव्यता मास फंक्शन पी (यू) च्या योगांशानुसार मोजली जाते.
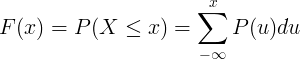
सतत वितरण सारणी
सतत वितरण म्हणजे सतत रँडम व्हेरिएबलचे वितरण.
सतत वितरण उदाहरण
...
सतत वितरण सारणी
| वितरणाचे नाव | वितरण प्रतीक | संभाव्यता घनता कार्य (पीडीएफ) | मीन | तफावत |
|---|---|---|---|---|
| एफ एक्स ( एक्स ) |
μ = ई ( एक्स ) |
σ 2 = वार ( एक्स ) |
||
| सामान्य / गौसी | एक्स ~ एन (μ, σ 2 ) |
|
μ | . 2 |
| एकसारखा | X ~ U ( a , b ) |
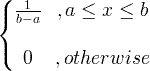 |
|
|
| घातांकीय | एक्स ~ क्स्प (λ) | |
|
|
| गामा | X ~ gamma ( c , λ) | 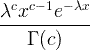 x / 0, c / 0, λ/ 0 |
|
|
| चि चौरस | एक्स ~ χ 2 ( के ) |
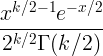 |
के |
2 के |
| विशार्ट | ||||
| एफ | एक्स ~ फॅ ( के 1 , के 2 ) |
|||
| बीटा | ||||
| वेइबुल | ||||
| लॉग-सामान्य | एक्स ~ एलएन (μ, σ 2 ) |
|||
| रेलेघ | ||||
| काउची | ||||
| दिरीचलेट | ||||
| लॅपलेस | ||||
| लेवी | ||||
| तांदूळ | ||||
| विद्यार्थ्यांची टी |
स्वतंत्र वितरण टेबल
स्वतंत्र वितरण म्हणजे वेगळ्या रँडम व्हेरिएबलचे वितरण.
स्वतंत्र वितरण उदाहरण
...
स्वतंत्र वितरण टेबल
| वितरणाचे नाव | वितरण प्रतीक | संभाव्यता मास फंक्शन (pmf) | मीन | तफावत | |
|---|---|---|---|---|---|
| f x ( के ) = पी ( एक्स = के ) के = 0,1,2, ... |
ई ( x ) | वार ( x ) | |||
| द्विपदी | एक्स ~ बिन ( एन , पी ) |
|
एनपी |
एनपी (1- पी ) |
|
| पोयसन | एक्स ~ पोयसन (λ) |
|
. ≥ 0 |
λ |
λ |
| एकसारखा | X ~ U ( a, b ) |
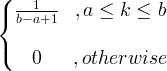 |
|
|
|
| भूमितीय | एक्स ~ जिओम ( पी ) |
|
|
|
|
| हायपर-भूमितीय | एक्स ~ एचजी ( एन , के , एन ) |
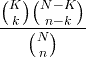 |
एन = 0,1,2, ... के = 0,1, .., एन एन = 0,1, ..., एन |
|
|
| बर्नौली | एक्स ~ बर्न ( p ) |
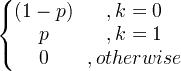 |
पी |
पी (1- पी ) |
|
हे देखील पहा
संभाव्यता आणि सांख्यिकी
वेगवान सारण्या