प्रमाणित विचलन
संभाव्यता आणि आकडेवारीमध्ये, यादृच्छिक चलचे प्रमाण विचलन म्हणजे क्षमतेच्या मूल्यापासून यादृच्छिक चलचे सरासरी अंतर.
हे रॅंडम व्हेरिएबल मधल्या मूल्याजवळ कसे वितरित केले जाते हे दर्शवते. लहान प्रमाणातील विचलन सूचित करते की यादृच्छिक व्हेरिएबल मधल्या मूल्याजवळ वितरित केले जाते. मोठे प्रमाण विचलन दर्शविते की यादृच्छिक व्हेरिएबल मधल्या मूल्यापासून खूपच जास्त वितरित केले जाते.
मानक विचलन परिभाषा सूत्र
मानक विचलन हे यादृच्छिक व्हेरिएबल एक्सच्या भिन्नतेचे चौरस मूळ आहे, ज्याचे मूल्य μ आहे.
![]()
आम्हाला मिळू शकणार्या प्रमाण विचलनाच्या परिभाषेतून
![]()
सतत यादृच्छिक चलचे मानक विचलन
मध्यम मूल्य value आणि संभाव्यता घनता फंक्शन एफ (एक्स) सह सतत यादृच्छिक चल करीता:
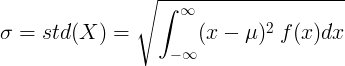
किंवा
![\ सिग्मा = एसटीडी (एक्स) = \ स्क्वेअर {\ डावीकडे [\ इंटी _ {- ty इन्फ्टी} ^ {\ इन्फ्टी} एक्स ^ 2 \: एफ (एक्स) डीएक्स \ राइट] - \ म्यू ^ 2}](standard_deviation/cont_std2.gif)
वेगळ्या यादृच्छिक चलचे मानक विचलन
मध्यम मूल्य with आणि संभाव्यता मास फंक्शन पी (एक्स) सह वेगवान यादृच्छिक चल एक्ससाठी:
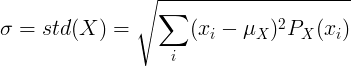
किंवा
![\ सिग्मा = एसटीडी (एक्स) = \ वर्गमीटर {\ बाकी [\ योग_ {i} ^ {_ x_i ^ 2 पी (x_i) \ उजवीकडे] - \ म्यू ^ 2}](standard_deviation/disc_std2.gif)
हे देखील पहा
संभाव्यता आणि सांख्यिकी
वेगवान सारण्या