मूलभूत संभाव्यता फॉर्म्युले

 

संभाव्यता श्रेणी

0 ≤ पी ( ए ) ≤ 1

पूरक घटनांचा नियम

पी ( ए सी ) + पी ( ए ) = 1

जोडण्याचा नियम

पी (एबीबी) = पी (ए) + पी (बी) - पी (एबीबी)

कार्यक्रम नाउमेद करा

इ आणि इव्हेंट्स iff निराश आहेत

पी (एबीबी) = 0

सशर्त संभाव्यता

पी (ए | बी) = पी (एबीबी) / पी (बी)

बायस फॉर्म्युला

पी (ए | बी) = पी (बी | ए) ⋅ पी (ए) / पी (बी)

स्वतंत्र कार्यक्रम

घटनाक्रम अ आणि बी स्वतंत्र आहेत तर

पी (ए∩बी) = पी (ए) ⋅ पी (बी)

संचयी वितरण कार्य

एफ एक्स ( एक्स ) = पी ( एक्स ≤ x )

संभाव्यता मास फंक्शन

बेरीज (i = 1..n, पी (एक्स = एक्स (आय)) = 1

संभाव्यता घनता कार्य

fX (x) = dFX (x) / dx

FX (x) = अविभाज्य (-inf..x, fX (y) * dy)

FX (x) = बेरीज (के = 1..x, पी (एक्स = के))

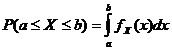
पी (ए <= एक्स <= बी) = अविभाज्य (ए..बी, एफएक्स (एक्स) * डीएक्स)

अविभाज्य (-inf..inf, fX (x) * dx) = 1

 

सहकार

कॉक्स (एक्स, वाय) = ई (एक्स-यूएक्स) (वाय-उय) = ई (एक्सवाय) - उक्स * यू

सहसंबंध

कॉर (एक्स, वाय) = कॉव्ह (एक्स, वाय) / (इयत्ता (एक्स) * इयत्ता (वाय))

 

बर्नौली: 0-अपयश 1-यश

भौमितिक: 0-अपयश 1-यश

हायपरजोमेट्रिक: के ऑब्जेक्ट्ससह एन ऑब्जेक्ट्स, एन ऑब्जेक्ट्स घेतली जातात.

 

 

 
 
संभाव्यता आणि सांख्यिकी
वेगवान सारण्या