e stała

Stała lub liczba Eulera jest stałą matematyczną. Stała e jest liczbą rzeczywistą i niewymierną.

e = 2,718281828459 ...

Definicja e
Właściwości E.
Podstawa e logarytm
Funkcja wykładnicza
Wzór Eulera

Definicja e

Stała e jest definiowana jako granica:

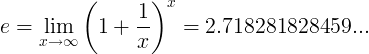
$e = \ lim_ {x \ rightarrow \ infty} \ left (1+ \ frac {1} {x} \ right) ^ x = 2,718281828459 ...$

Alternatywne definicje

Stała e jest definiowana jako granica:

$e = \ lim_ {x \ rightarrow 0} \ left (1+ \ right x) ^ \ frac {1} {x}$

Stała e jest zdefiniowana jako nieskończony szereg:

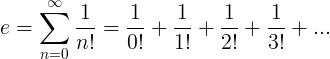
$e = \ sum_ {n = 0} ^ {\ infty} \ frac {1} {n!} = \ frac {1} {0!} + \ frac {1} {1!} + \ frac {1} { 2!} + \ Frac {1} {3!} + ...$

Właściwości E.

Wzajemność e

Odwrotność e jest granicą:

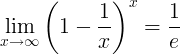
$\ lim_ {x \ rightarrow \ infty} \ left (1- \ frac {1} {x} \ right) ^ x = \ frac {1} {e}$

Pochodne E.

Pochodną funkcji wykładniczej jest funkcja wykładnicza:

( e ^x ) '= e ^x

Pochodną funkcji logarytmu naturalnego jest funkcja odwrotna:

(log _e x ) '= (ln x )' = 1 / x

Całki e

Całka nieoznaczona funkcji wykładniczej e ^x jest funkcją wykładniczą e ^x .

∫ e ^x dx = e ^x + c

Całka nieoznaczona funkcji logarytmu naturalnego log _e x wynosi:

∫ log _e x dx = ∫ ln x dx = x ln x - x + c

Całka oznaczona od 1 do e funkcji odwrotności 1 / x wynosi 1:

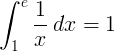
$\ int_ {1} ^ {e} \ frac {1} {x} \: dx = 1$

Podstawa e logarytm

Logarytm naturalny liczby x jest definiowany jako logarytm podstawowy e z x:

ln x = log _e x

Funkcja wykładnicza

Funkcja wykładnicza jest zdefiniowana jako:

f ( x ) = exp ( x ) = e ^x

Wzór Eulera

Liczba zespolona e ^iθ ma tożsamość:

e ^iθ = cos ( θ ) + i sin ( θ )

i jest jednostką urojoną (pierwiastek kwadratowy z -1).

θ to dowolna liczba rzeczywista.