Reguły wykładników
Reguły wykładników, prawa wykładników i przykłady.
Co to jest wykładnik
Podstawa a podniesiona do potęgi n jest równa pomnożeniu a, n razy:
a n = a × a × ... × a
n razy
a jest podstawą, a n jest wykładnikiem.
Przykłady
3 1 = 3
3 2 = 3 × 3 = 9
3 3 = 3 × 3 × 3 = 27
3 4 = 3 × 3 × 3 × 3 = 81
3 5 = 3 × 3 × 3 × 3 × 3 = 243
Zasady i właściwości wykładników
| Nazwa reguły | Reguła | Przykład |
|---|---|---|
| Zasady dotyczące produktów | a n ⋅ a m = a n + m | 2 3 ⋅ 2 4 = 2 3 + 4 = 128 |
| a n ⋅ b n = ( a ⋅ b ) n | 3 2 ⋅ 4 2 = (3⋅4) 2 = 144 | |
| Reguły ilorazowe | a n / a m = a n - m | 2 5 /2 3 = 2 5-3 = 4 |
| a n / b n = ( a / b ) n | 4 3 /2 3 = (4/2), 3 = 8 | |
| Zasady mocy | ( b n ) m = b n⋅m | (2 3 ) 2 = 2 3⋅2 = 64 |
| b n m = b ( n m ) | 2 3 2 = 2 ( 3 2 ) = 512 | |
| m √ ( b n ) = b n / m | 2 √ (2 6 ) = 2 6/2 = 8 | |
| b 1 / n = n √ b | 8 1/3 = 3 √ 8 = 2 | |
| Ujemne wykładniki | b -n = 1 / b n | 2 -3 = 1/2 3 = 0.125 |
| Zero zasad | b 0 = 1 | 5 0 = 1 |
| 0 n = 0, dla n / 0 | 0 5 = 0 | |
| Jedna zasada | b 1 = b | 5 1 = 5 |
| 1 n = 1 | 1 5 = 1 | |
| Zasada minus jeden | 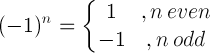 |
(-1) 5 = -1 |
| Reguła pochodna | ( x n ) ' = n ⋅ x n -1 | ( x 3 ) ' = 3⋅ x 3-1 |
| Reguła całkowa | ∫ x n dx = x n +1 / ( n +1) + C | ∫ x 2 dx = x 2 + 1 / (2 + 1) + C |
Reguły dotyczące wykładników
Reguła dotycząca produktu o tej samej podstawie
a n ⋅ a m = a n + m
Przykład:
2 3 ⋅ 2 4 = 2 3 + 4 = 2 7 = 2⋅2⋅2⋅2⋅2⋅2⋅2 = 128
Reguła iloczynu z tym samym wykładnikiem
a n ⋅ b n = ( a ⋅ b ) n
Przykład:
3 2 ⋅ 4 2 = (3⋅4) 2 = 12 2 = 12⋅12 = 144
Zobacz: Mnożenie wykładników
Zasady ilorazu wykładników
Reguła ilorazu o tej samej podstawie
a n / a m = a n - m
Przykład:
2 5 /2 3 = 2 3/5 = 2, 2 = 2⋅2 = 4
Reguła ilorazu z tym samym wykładnikiem
a n / b n = ( a / b ) n
Przykład:
4 3 /2 3 = (4/2), 3 = 2, 3 = 2⋅2⋅2 = 8
Zobacz: Dzielenie wykładników
Reguły potęgi wykładników
Reguła władzy I.
( a n ) m = a n⋅m
Przykład:
(2 3 ) 2 = 2 3⋅2 = 2 6 = 2⋅2⋅2⋅2⋅2⋅2 = 64
Reguła władzy II
a n m = a ( n m )
Przykład:
2 3 2 = 2 (3 2 ) = 2 (3⋅3) = 2 9 = 2⋅2⋅2⋅2⋅2⋅2⋅2⋅2⋅2 = 512
Władza rządzi radykałami
m √ ( a n ) = a n / m
Przykład:
2 √ (2 6 ) = 2 6/2 = 2 3 = 2⋅2⋅2 = 8
Reguła ujemnych wykładników
b -n = 1 / b n
Przykład:
2 -3 = 1/2 3 = 1 / (2⋅2⋅2) = 1/8 = 0.125
Zobacz: Wykładniki ujemne
Zobacz też
- Dodawanie wykładników
- Dzielenie wykładników
- Ułamkowe wykładniki
- Mnożenie wykładników
- Ujemne wykładniki
- Upraszczanie wykładników
- Wykładnik zerowy
- Kalkulator wykładników
- Kalkulator logarytmów
- Kalkulator wzrostu wykładniczego
- Kalkulator Antylogów
- log (x) rules
- Reguły ln (x)
- e stała