Numer zerowy (0)
- Definicja liczby zerowej
- Historia liczb zerowych
- Właściwości liczb zerowych
- Zestawy zawierające zero
Definicja liczby zerowej
Zero to liczba używana w matematyce do opisania braku lub zerowej ilości.
Kiedy na stole są 2 jabłka i bierzemy 2 jabłka, możemy powiedzieć, że na stole nie ma jabłek.
Liczba zerowa nie jest liczbą dodatnią ani liczbą ujemną.
Zero jest również symbolem zastępczym w innych liczbach (np .: 40,103, 170).
Czy zero to liczba?
Zero to liczba. Nie jest liczbą dodatnią ani ujemną.
Cyfra zerowa
Cyfra zerowa jest używana jako symbol zastępczy podczas pisania liczb.
Na przykład:
204 = 2 × 100 + 0 × 10 + 4 × 1
Historia liczb zerowych
Kto wymyślił liczbę zerową?
Współczesny symbol 0 został wynaleziony w Indiach w VI wieku, używany później przez Persów i Arabów, a później w Europie.
Symbol zera
Liczba zerowa jest oznaczona symbolem 0 .
W systemie cyfr arabskich używa się symbolu ٠.
Właściwości liczb zerowych
x oznacza dowolną liczbę.
| Operacja | Reguła | Przykład |
|---|---|---|
Dodanie |
x + 0 = x |
3 + 0 = 3 |
Odejmowanie |
x - 0 = x |
3 - 0 = 3 |
Mnożenie |
x × 0 = 0 |
5 × 0 = 0 |
Podział |
0 ÷ x = 0 , gdy x ≠ 0 |
0 ÷ 5 = 0 |
| x ÷ 0 jest niezdefiniowane |
5 ÷ 0 jest niezdefiniowane |
|
Potęgowanie |
0 x = 0 |
0 5 = 0 |
| x 0 = 1 |
5 0 = 1 |
|
Korzeń |
√ 0 = 0 |
|
Logarytm |
log b (0) jest niezdefiniowane |
|
| |
||
Factorial |
0! = 1 |
|
Sinus |
sin 0º = 0 |
|
Cosinus |
cos 0º = 1 |
|
Tangens |
tan 0º = 0 |
|
Pochodna |
0 '= 0 |
|
Całka |
∫ 0 d x = 0 + C |
|
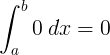 |
Zero dodatku
Dodanie liczby plus zero jest równe liczbie:
x + 0 = x
Na przykład:
5 + 0 = 5
Odejmowanie zera
Odejmowanie liczby minus zero jest równe liczbie:
x - 0 = x
Na przykład:
5 - 0 = 5
Mnożenie przez zero
Mnożenie liczby razy zero jest równe zero:
x × 0 = 0
Na przykład:
5 × 0 = 0
Liczba podzielona przez zero
Dzielenie liczby przez zero nie jest zdefiniowane:
x ÷ 0 jest niezdefiniowane
Na przykład:
5 ÷ 0 jest niezdefiniowane
Zero podzielone przez liczbę
Dzielenie zera przez liczbę to zero:
0 ÷ x = 0
Na przykład:
0 ÷ 5 = 0
Liczba do potęgi zerowej
Potęga liczby podniesionej przez zero wynosi jeden:
x 0 = 1
Na przykład:
5 0 = 1
Logarytm zera
Podstawowy logarytm b zero jest niezdefiniowany:
log b (0) jest niezdefiniowane
Nie ma liczby, o którą możemy podnieść podstawę b, aby uzyskać zero.
Jedynie granica logarytmu podstawy b z x, gdy x zbiega się do zera, jest minus nieskończoność:
![]()
Zestawy zawierające zero
Zero jest elementem liczb naturalnych, liczb całkowitych, liczb rzeczywistych i zbiorów liczb zespolonych:
| Zestaw | Ustaw zapis członkostwa |
|---|---|
| Liczby naturalne (nieujemne) | 0 ∈ ℕ 0 |
| Liczby całkowite | 0 ∈ ℤ |
| Liczby rzeczywiste | 0 ∈ ℝ |
| Liczby zespolone | 0 ∈ ℂ |
| Liczby wymierne | 0 ∈ ℚ |
Czy zero jest liczbą parzystą czy nieparzystą?
Zbiór liczb parzystych to:
{..., -10, -8, -6, -4, -2, 0, 2, 4, 6, 8, 10, ...}
Zbiór liczb nieparzystych to:
{..., -9, -7, -5, -3, -1, 1, 3, 5, 7, 9, ...}
Zero jest całkowitą wielokrotnością 2:
0 × 2 = 0
Zero należy do zbioru liczb parzystych:
0 ∈ {2 k , k ∈ℤ}
Zatem zero jest liczbą parzystą, a nie liczbą nieparzystą.
Czy zero jest liczbą naturalną?
Istnieją dwie definicje zbioru liczb naturalnych.
Zbiór nieujemnych liczb całkowitych:
ℕ 0 = {0,1,2,3,4,5,6,7,8, ...}
Zbiór dodatnich liczb całkowitych:
ℕ 1 = {1, 2, 3, 4, 5, 6, 7, 8, ...}
Zero należy do zbioru nieujemnych liczb całkowitych:
0 ∈ ℕ 0
Zero nie należy do zbioru dodatnich liczb całkowitych:
0 ∉ ℕ 1
Czy zero jest liczbą całkowitą?
Istnieją trzy definicje liczb całkowitych:
Zbiór liczb całkowitych:
ℤ = {0,1,2,3,4,5,6,7,8, ...}
Zbiór nieujemnych liczb całkowitych:
ℕ 0 = {0,1,2,3,4,5,6,7,8, ...}
Zbiór dodatnich liczb całkowitych:
ℕ 1 = {1, 2, 3, 4, 5, 6, 7, 8, ...}
Zero jest członkiem zbioru liczb całkowitych i zbioru nieujemnych liczb całkowitych:
0 ∈ ℤ
0 ∈ ℕ 0
Zero nie należy do zbioru dodatnich liczb całkowitych:
0 ∉ ℕ 1
Czy zero jest liczbą całkowitą?
Zbiór liczb całkowitych:
ℤ = {0,1,2,3,4,5,6,7,8, ...}
Zero należy do zbioru liczb całkowitych:
0 ∈ ℤ
Zatem zero jest liczbą całkowitą.
Czy zero jest liczbą wymierną?
Liczba wymierna to liczba, którą można wyrazić jako iloraz dwóch liczb całkowitych:
ℚ = { n / m ; n , m ∈ℤ}
Zero można zapisać jako iloraz dwóch liczb całkowitych.
Na przykład:
0 = 0/3
Zatem zero jest liczbą wymierną.
Czy zero jest liczbą dodatnią?
Liczbę dodatnią definiuje się jako liczbę większą od zera:
x / 0
Na przykład:
5/ 0
Ponieważ zero nie jest większe od zera, nie jest liczbą dodatnią.
Czy zero jest liczbą pierwszą?
Liczba 0 nie jest liczbą pierwszą.
Zero nie jest liczbą dodatnią i ma nieskończoną liczbę dzielników.
Najniższa liczba pierwsza to 2.