Wartość oczekiwana
W prawdopodobieństwie i statystyce wartość oczekiwana lub wartość oczekiwana to średnia ważona wartość zmiennej losowej.
Oczekiwanie ciągłej zmiennej losowej
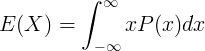
E ( X ) jest wartością oczekiwaną ciągłej zmiennej losowej X
x jest wartością ciągłej zmiennej losowej X
P ( x ) jest funkcją gęstości prawdopodobieństwa
Oczekiwanie dyskretnej zmiennej losowej
![]()
E ( X ) jest wartością oczekiwaną ciągłej zmiennej losowej X
x jest wartością ciągłej zmiennej losowej X
P ( x ) jest funkcją masy prawdopodobieństwa X
Właściwości oczekiwania
Liniowość
Gdy a jest stałe, a X, Y to zmienne losowe:
E ( aX ) = aE ( X )
E ( X + Y ) = E ( X ) + E ( Y )
Stały
Gdy c jest stałe:
E ( c ) = c
Produkt
Gdy X i Y są niezależnymi zmiennymi losowymi:
E ( X ⋅Y ) = E ( X ) ⋅ E ( Y )
warunkowe oczekiwanie
Zobacz też
PRAWDOPODOBIEŃSTWO I STATYSTYKA
- Podstawowe prawdopodobieństwo
- Oczekiwanie
- Zmienność
- Odchylenie standardowe
- Rozkład prawdopodobieństwa
- Normalna dystrybucja
- Symbole statystyk
SZYBKIE STOŁY