Zmienność

W prawdopodobieństwie i statystyce wariancja zmiennej losowej jest średnią wartością kwadratu odległości od wartości średniej. Reprezentuje rozkład zmiennej losowej w pobliżu wartości średniej. Mała wariancja wskazuje, że zmienna losowa ma rozkład w pobliżu wartości średniej. Duża wariancja wskazuje, że zmienna losowa jest rozłożona daleko od wartości średniej. Na przykład przy rozkładzie normalnym wąska krzywa dzwonowa będzie miała małą wariancję, a szeroka krzywa dzwonowa będzie miała dużą wariancję.

Definicja wariancji

Wariancja zmiennej losowej X jest oczekiwaną wartością kwadratów różnicy X i wartości oczekiwanej μ.

σ ² = Var ( X ) = E [( X - μ ) ² ]

Z definicji wariancji możemy otrzymać

σ ² = Var ( X ) = E ( X ² ) - μ ²

Wariancja ciągłej zmiennej losowej

Dla ciągłej zmiennej losowej o średniej wartości μ i funkcji gęstości prawdopodobieństwa f (x):

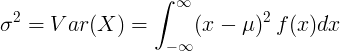
$\ sigma ^ 2 = Var (X) = \ int _ {- \ infty} ^ {\ infty} (x- \ mu) ^ 2 \: f (x) dx$

lub

$Var (X) = \ left [\ int _ {- \ infty} ^ {\ infty} x ^ 2 \: f (x) dx \ right] - \ mu ^ 2$

Wariancja dyskretnej zmiennej losowej

Dla dyskretnej zmiennej losowej X o wartości średniej μ i funkcji masy prawdopodobieństwa P (x):

$\ sigma ^ 2 = Var (X) = \ sum_ {i} ^ {} (x_i- \ mu _X) ^ 2P_X (x_i)$

lub

$Var (X) = \ left [\ sum_ {i} ^ {} x_i ^ 2P (x_i) \ right] - \ mu ^ 2$

Własności wariancji

Gdy X i Y są niezależnymi zmiennymi losowymi:

Var ( X + Y ) = Var ( X ) + Var ( Y )

Odchylenie standardowe ►

Zmienność

Definicja wariancji

Wariancja ciągłej zmiennej losowej

Wariancja dyskretnej zmiennej losowej

Własności wariancji

Var ( X + Y ) = Var ( X ) + Var ( Y )

Zobacz też

PRAWDOPODOBIEŃSTWO I STATYSTYKA

SZYBKIE STOŁY