Rozkład prawdopodobieństwa
W prawdopodobieństwie i statystyce rozkład jest cechą zmiennej losowej, opisuje prawdopodobieństwo zmiennej losowej w każdej wartości.
Każdy rozkład ma pewną funkcję gęstości prawdopodobieństwa i funkcję rozkładu prawdopodobieństwa.
Chociaż istnieje nieokreślona liczba rozkładów prawdopodobieństwa, istnieje kilka najczęściej używanych rozkładów.
Dystrybuanta
Rozkład prawdopodobieństwa jest opisany skumulowaną funkcją rozkładu F (x),
czyli prawdopodobieństwo, że zmienna losowa X uzyska wartość mniejszą lub równą x:
F ( x ) = P ( X ≤ x )
Ciągła dystrybucja
Dystrybuanta F (x) oblicza się przez całkowanie funkcji gęstości prawdopodobieństwa f (u) ciągłej zmiennej losowej X.
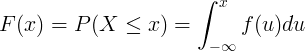
Dystrybucja dyskretna
Dystrybucję skumulowaną F (x) oblicza się przez zsumowanie funkcji masy prawdopodobieństwa P (u) dyskretnej zmiennej losowej X.
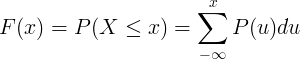
Tabela dystrybucji ciągłych
Rozkład ciągły to rozkład ciągłej zmiennej losowej.
Przykład dystrybucji ciągłej
...
Tabela dystrybucji ciągłych
| Nazwa dystrybucji | Symbol dystrybucji | Funkcja gęstości prawdopodobieństwa (pdf) | Oznaczać | Zmienność |
|---|---|---|---|---|
| f X ( x ) |
μ = E ( X ) |
σ 2 = Var ( X ) |
||
| Normalny / Gaussa | X ~ N (μ, σ 2 ) |
|
μ | σ 2 |
| Mundur | X ~ U ( a , b ) |
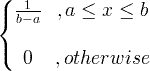 |
|
|
| Wykładniczy | X ~ exp (λ) | |
|
|
| Gamma | X ~ gamma ( c , λ) | 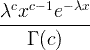 x / 0, c / 0, λ/ 0 |
|
|
| Chi kwadrat | X ~ χ 2 ( k ) |
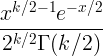 |
k |
2 tys |
| Wishart | ||||
| F | X ~ F ( k 1 , k 2 ) |
|||
| Beta | ||||
| Weibull | ||||
| Log-normalny | X ~ LN (μ, σ 2 ) |
|||
| Rayleigh | ||||
| Cauchy | ||||
| Dirichlet | ||||
| Laplace | ||||
| Nałożyć | ||||
| Ryż | ||||
| Student's t |
Tabela dystrybucji dyskretnych
Dystrybucja dyskretna to rozkład dyskretnej zmiennej losowej.
Przykład dystrybucji dyskretnej
...
Tabela dystrybucji dyskretnych
| Nazwa dystrybucji | Symbol dystrybucji | Funkcja masy prawdopodobieństwa (pmf) | Oznaczać | Zmienność | |
|---|---|---|---|---|---|
| f x ( k ) = P ( X = k ) k = 0, 1, 2, ... |
E ( x ) | Var ( x ) | |||
| Dwumianowy | X ~ Bin ( n , p ) |
|
np |
np (1- p ) |
|
| Poissona | X ~ Poissona (λ) |
|
λ ≥ 0 |
λ |
λ |
| Mundur | X ~ U ( a, b ) |
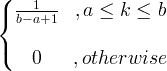 |
|
|
|
| Geometryczny | X ~ Geom ( p ) |
|
|
|
|
| Hiper-geometryczny | X ~ HG ( N , K , n ) |
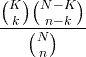 |
N = 0, 1, 2, ... K = 0, 1, .., N n = 0, 1, ..., N. |
|
|
| Bernoulli | X ~ Berno ( p ) |
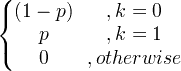 |
p |
p (1 p ) |
|
Zobacz też
PRAWDOPODOBIEŃSTWO I STATYSTYKA
- Podstawowe prawdopodobieństwo
- Oczekiwanie
- Zmienność
- Odchylenie standardowe
- Rozkład prawdopodobieństwa
- Normalna dystrybucja
- Symbole statystyk
SZYBKIE STOŁY