Podstawowe wzory prawdopodobieństwa

 

Zakres prawdopodobieństwa

0 ≤ P ( A ) ≤ 1

Reguła wydarzeń uzupełniających

P ( A C ) + P ( A ) = 1

Zasada dodawania

P (A∪B) = P (A) + P (B) - P (A∩B)

Rozłączne wydarzenia

Zdarzenia A i B są rozłączne iff

P (A∩B) = 0

Warunkowe prawdopodobieństwo

P (A | B) = P (A∩B) / P (B)

Formuła Bayesa

P (A | B) = P (B | A) ⋅ P (A) / P (B)

Niezależne wydarzenia

Zdarzenia A i B są niezależne iff

P (A∩B) = P (A) ⋅ P (B)

Dystrybuanta

F X ( x ) = P ( X ≤ x )

Prawdopodobieństwo funkcji masowej

sum (i = 1..n, P (X = x (i)) = 1

Funkcja gęstości prawdopodobieństwa

fX (x) = dFX (x) / dx

FX (x) = całka (-inf..x, fX (y) * dy)

FX (x) = suma (k = 1..x, P (X = k))

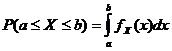
P (a <= X <= b) = całka (a..b, fX (x) * dx)

całka (-inf..inf, fX (x) * dx) = 1

 

Kowariancja

Cox (X, Y) = E (X-ux) (Y-uy) = E (XY) - ux * uy

Korelacja

corr (X, Y) = Cov (X, Y) / (Std (X) * Std (Y))

 

Bernoulli: 0-porażka 1-sukces

Geometryczny: 0-niepowodzenie 1-sukces

Hipergeometric: N obiektów z K obiektami powodzenia, n obiektów jest branych.

 

 

 
 
PRAWDOPODOBIEŃSTWO I STATYSTYKA
SZYBKIE STOŁY