Функция Arccos (x)
Arccos (x), cos -1 (x), функция обратного косинуса .
Определение Arccos
Арккосинус x определяется как функция, обратная косинусу x, когда -1≤x≤1.
Когда косинус y равен x:
cos y = x
Тогда арккосинус x равен функции обратного косинуса x, которая равна y:
arccos x = cos -1 x = y
(Здесь cos -1 x означает обратный косинус и не означает косинус в степени -1).
пример
arccos 1 = cos -1 1 = 0 рад = 0 °
График arccos
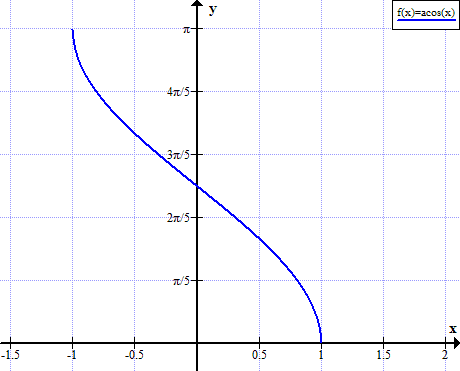
Правила Arccos
| Название правила | Правило |
|---|---|
| Косинус арккозина | cos (arccos x ) = x |
| Арккосинус косинуса | arccos (cos x ) = x + 2 k π, когда k ∈ℤ ( k целое) |
| Arccos отрицательного аргумента | arccos (- x ) = π - arccos x = 180 ° - arccos x |
| Дополнительные углы | arccos x = π / 2 - arcsin x = 90 ° - arcsin x |
| Сумма Arccos | arccos ( α ) + arccos ( β ) = arccos ( αβ - √ (1- α 2 ) (1- β 2 ) ) |
| Разница в Arccos | arccos ( α ) - arccos ( β ) = arccos ( αβ + √ (1- α 2 ) (1- β 2 ) ) |
| Arccos греха х | arccos (sin x ) = - x - (2 k +0,5) π |
| Синус арккозина | |
| Тангенс арккосинуса |  |
| Производная арккозина | 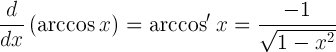 |
| Неопределенный интеграл арккосинуса | |
Таблица Arccos
| х | arccos (x) (рад) |
arccos (x) (°) |
|---|---|---|
| -1 | π | 180 ° |
| -√ 3 /2 | 5π / 6 | 150 ° |
| -√ 2 /2 | 3π / 4 | 135 ° |
| -1/2 | 2π / 3 | 120 ° |
| 0 | π / 2 | 90 ° |
| 1/2 | π / 3 | 60 ° |
| √ 2 /2 | π / 4 | 45 ° |
| √ 3 /2 | π / 6 | 30 ° |
| 1 | 0 | 0 ° |
Смотрите также
- Функция косинуса
- Функция арксинуса
- Арктанфункция
- Калькулятор Arccos
- Конвертер радианов в градусы
- Arccos из 0
- Arccos из 1
- Arccos из 2
- Аркко из 3
- Арккос Кос
- Arccos греха
- Производная от Arccos
- График Arccos
- Cos of Arccos
- Грех arccos
- Загар аркко