లోగరిథం నియమాలు

బేస్ బి సంవర్గమానం అనేక ఉంది విశేషము మేము పెంచడానికి అవసరమైన బేస్ సంఖ్య పొందడానికి.

• లోగరిథం నిర్వచనం
• లోగరిథం నియమాలు
• లోగరిథం సమస్యలు
• కాంప్లెక్స్ లోగరిథం
• లాగ్ యొక్క గ్రాఫ్ (x)
• లోగరిథం పట్టిక
• లోగరిథం కాలిక్యులేటర్

లోగరిథం నిర్వచనం

B ను y యొక్క శక్తికి పెంచినప్పుడు సమాన x:

b ^y = x

అప్పుడు x యొక్క బేస్ బి లాగరిథం y కి సమానం:

లాగ్ _b ( x ) = y

ఉదాహరణకు ఎప్పుడు:

2 ⁴ = 16

అప్పుడు

లాగ్ ₂ (16) = 4

ఎక్స్‌పోనెన్షియల్ ఫంక్షన్ యొక్క విలోమ ఫంక్షన్‌గా లోగరిథం

లాగరిథమిక్ ఫంక్షన్,

y = లాగ్ _బి ( x )

ఘాతాంక ఫంక్షన్ యొక్క విలోమ ఫంక్షన్,

x = b ^y

కాబట్టి మనం x (x/ 0) యొక్క లాగరిథం యొక్క ఘాతాంక ఫంక్షన్‌ను లెక్కిస్తే,

f ( f ^-1 ( x )) = b ^లాగ్ b ^{( x )} = x

లేదా x యొక్క ఘాతాంక ఫంక్షన్ యొక్క లాగరిథంను లెక్కిస్తే,

f ^-1 ( f ( x )) = లాగ్ _b ( b ^x ) = x

సహజ లాగరిథం (ln)

సహజ లాగరిథం బేస్ e కు లాగరిథం:

ln ( x ) = లాగ్ _ఇ ( x )

ఇ స్థిరాంకం సంఖ్య అయినప్పుడు :

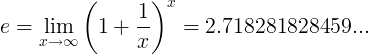
లేదా

 

చూడండి: సహజ లాగరిథం

విలోమ లోగరిథం లెక్కింపు

విలోమ లోగరిథం (లేదా యాంటీ లోగరిథం) బేస్ బి ను లాగరిథం y కి పెంచడం ద్వారా లెక్కించబడుతుంది:

x = లాగ్ ^-1 ( y ) = b ^y

లోగరిథమిక్ ఫంక్షన్

లాగరిథమిక్ ఫంక్షన్ యొక్క ప్రాథమిక రూపం:

f ( x ) = లాగ్ _బి ( x )

లోగరిథం నియమాలు

నియమం పేరు	నియమం
లోగరిథం ఉత్పత్తి నియమం	log b ( x y ) = log b ( x ) + log b ( y )
లోగరిథం కోటీన్ నియమం	log b ( x / y ) = log b ( x ) - log b ( y )
లోగరిథం శక్తి నియమం	log b ( x y ) = y log b ( x )
లోగరిథం బేస్ స్విచ్ నియమం	లాగ్ బి ( సి ) = 1 / లాగ్ సి ( బి )
లోగరిథం బేస్ మార్పు నియమం	log b ( x ) = log c ( x ) / log c ( b )
లోగరిథం యొక్క ఉత్పన్నం	f ( x ) = లాగ్ బి ( x ) ⇒ f ' ( x ) = 1 / ( x ln ( బి ))
లోగరిథం యొక్క సమగ్ర	∫ log b ( x ) dx = x ∙ (log b ( x ) - 1 / ln ( b ) ) + C
ప్రతికూల సంఖ్య యొక్క లోగరిథం	x ≤ 0 ఉన్నప్పుడు లాగ్ బి ( x ) నిర్వచించబడలేదు
0 యొక్క లోగరిథం	లాగ్ బి (0) నిర్వచించబడలేదు
1 యొక్క లోగరిథం	లాగ్ బి (1) = 0
బేస్ యొక్క లోగరిథం	లాగ్ బి ( బి ) = 1
అనంతం యొక్క లోగరిథం	లిమ్ లాగ్ బి ( x ) = ∞, ఉన్నప్పుడు x → ∞

చూడండి: లోగరిథం నియమాలు

 

లోగరిథం ఉత్పత్తి నియమం

X మరియు y యొక్క గుణకారం యొక్క లోగరిథం x యొక్క లోగరిథం మరియు y యొక్క లాగరిథం యొక్క మొత్తం.

log _b ( x y ) = log _b ( x ) + log _b ( y )

ఉదాహరణకి:

లాగ్ ₁₀ (3 ∙ 7) = లాగ్ ₁₀ (3) + లాగ్ ₁₀ (7)

లోగరిథం కోటీన్ నియమం

X మరియు y యొక్క విభజన యొక్క లోగరిథం x యొక్క లోగరిథం మరియు y యొక్క లోగరిథం యొక్క వ్యత్యాసం.

log _b ( x / y ) = log _b ( x ) - log _b ( y )

ఉదాహరణకి:

లాగిన్ ₁₀ (3 / 7) = log ₁₀ (3) - లాగిన్ ₁₀ (7)

లోగరిథం శక్తి నియమం

Y యొక్క శక్తికి పెంచబడిన x యొక్క లాగరిథం x యొక్క లాగరిథం కంటే y రెట్లు ఎక్కువ.

log _b ( x ^y ) = y log _b ( x )

ఉదాహరణకి:

లాగిన్ ₁₀ (2 ⁸ ) = 8 ∙ లాగిన్ ₁₀ (2)

లోగరిథం బేస్ స్విచ్ నియమం

సి యొక్క బేస్ బి లోగరిథం 1 యొక్క బేస్ సి లాగరిథం ద్వారా విభజించబడింది.

లాగ్ _బి ( సి ) = 1 / లాగ్ _సి ( బి )

ఉదాహరణకి:

లాగ్ ₂ (8) = 1 / లాగ్ ₈ (2)

లోగరిథం బేస్ మార్పు నియమం

X యొక్క బేస్ బి లోగరిథం x యొక్క బేస్ సి లాగరిథం, బి యొక్క సి సి లాగరిథం ద్వారా విభజించబడింది.

log _b ( x ) = log _c ( x ) / log _c ( b )

ఉదాహరణకు, కాలిక్యులేటర్‌లో లాగ్ ₂ (8) ను లెక్కించడానికి, మేము బేస్ 10 కి మార్చాలి:

లాగ్ ₂ (8) = లాగ్ ₁₀ (8) / లాగ్ ₁₀ (2)

చూడండి: లాగ్ బేస్ మార్పు నియమం

ప్రతికూల సంఖ్య యొక్క లోగరిథం

X ప్రతికూలంగా ఉన్నప్పుడు లేదా సున్నాకి సమానమైనప్పుడు x <= 0 నిర్వచించబడనప్పుడు x యొక్క బేస్ బి రియల్ లాగరిథం:

x ≤ 0 ఉన్నప్పుడు లాగ్ _బి ( x ) నిర్వచించబడలేదు

చూడండి: ప్రతికూల సంఖ్య యొక్క లాగ్

0 యొక్క లోగరిథం

సున్నా యొక్క బేస్ బి లాగరిథం నిర్వచించబడలేదు:

లాగ్ _బి (0) నిర్వచించబడలేదు

X యొక్క మూల బి లాగరిథం యొక్క పరిమితి, x సున్నాకి చేరుకున్నప్పుడు, మైనస్ అనంతం:

చూడండి: సున్నా యొక్క లాగ్

1 యొక్క లోగరిథం

ఒకదాని యొక్క బేస్ బి లాగరిథం సున్నా:

లాగ్ _బి (1) = 0

ఉదాహరణకు, టెహ్ బేస్ రెండు లాగరిథం ఒకటి సున్నా:

లాగ్ ₂ (1) = 0

చూడండి: ఒక లాగ్

అనంతం యొక్క లోగరిథం

X యొక్క బేస్ బి లాగరిథం యొక్క పరిమితి, x అనంతానికి చేరుకున్నప్పుడు, అనంతానికి సమానం:

లిమ్ లాగ్ _బి ( x ) = ∞, ఉన్నప్పుడు x → ∞

చూడండి: అనంతం యొక్క చిట్టా

బేస్ యొక్క లోగరిథం

B యొక్క బేస్ బి లాగరిథం ఒకటి:

లాగ్ _బి ( బి ) = 1

ఉదాహరణకు, రెండు యొక్క రెండు లాగరిథం ఒకటి:

లాగ్ ₂ (2) = 1

లోగరిథం ఉత్పన్నం

ఎప్పుడు

f ( x ) = లాగ్ _బి ( x )

అప్పుడు f (x) యొక్క ఉత్పన్నం:

f ' ( x ) = 1 / ( x ln ( b ))

చూడండి: లాగ్ ఉత్పన్నం

లోగరిథం సమగ్ర

X యొక్క లాగరిథం యొక్క సమగ్ర:

∫ log _b ( x ) dx = x ∙ (log _b ( x ) - 1 / ln ( b ) ) + C

ఉదాహరణకి:

∫ లాగ్ ₂ ( x ) dx = x ∙ (లాగ్ ₂ ( x ) - 1 / ln (2) ) + సి

లోగరిథం ఉజ్జాయింపు

లాగ్ ₂ ( x ) ≈ n + ( x / 2 ⁿ - 1),

కాంప్లెక్స్ లోగరిథం

సంక్లిష్ట సంఖ్య z కోసం:

z = re ^iθ = x + iy

సంక్లిష్ట లాగరిథం ఉంటుంది (n = ...- 2, -1,0,1,2, ...):

లాగ్ z = ln ( r ) + i ( θ + 2nπ ) = ln ( x ( x ² + y ² )) + i · arctan ( y / x ))

లోగరిథం సమస్యలు మరియు సమాధానాలు

సమస్య # 1

కోసం x ను కనుగొనండి

లాగ్ ₂ ( x ) + లాగ్ ₂ ( x -3) = 2

పరిష్కారం:

ఉత్పత్తి నియమాన్ని ఉపయోగించడం:

లాగ్ ₂ ( x ( x -3)) = 2

లాగరిథం నిర్వచనం ప్రకారం లోగరిథం రూపాన్ని మార్చడం:

x ( x -3) = 2 ²

లేదా

x ² -3 x -4 = 0

వర్గ సమీకరణాన్ని పరిష్కరించడం:

x _1,2 = [3 ± √ (9 + 16)] / 2 = [3 ± 5] / 2 = 4, -1

లాగరిథం ప్రతికూల సంఖ్యల కోసం నిర్వచించబడనందున, సమాధానం:

x = 4

సమస్య # 2

కోసం x ను కనుగొనండి

లాగ్ ₃ ( x +2) - లాగ్ ₃ ( x ) = 2

పరిష్కారం:

కొటెంట్ నియమాన్ని ఉపయోగించడం:

లాగ్ ₃ (( x +2) / x ) = 2

లాగరిథం నిర్వచనం ప్రకారం లోగరిథం రూపాన్ని మార్చడం:

( x +2) / x = 3 ²

లేదా

x +2 = 9 x

లేదా

8 x = 2

లేదా

x = 0.25

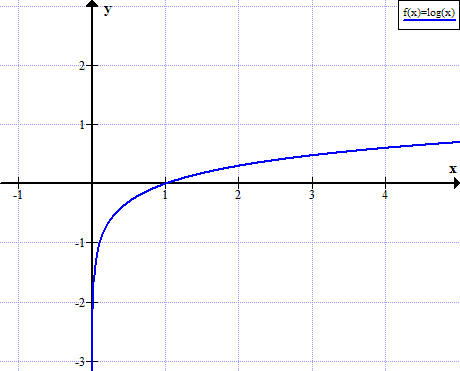
లాగ్ యొక్క గ్రాఫ్ (x)

x యొక్క నిజమైన సానుకూల విలువలకు లాగ్ (x) నిర్వచించబడలేదు:

లోగరిథమ్స్ పట్టిక

x	లాగ్ 10 x	లాగ్ 2 x	లాగ్ ఇ x
0	నిర్వచించబడలేదు	నిర్వచించబడలేదు	నిర్వచించబడలేదు
0 +	-	-	-
0.0001	-4	-13.287712	-9.210340
0.001	-3	-9.965784	-6.907755
0.01	-2	-6.643856	-4.605170
0.1	-1	-3.321928	-2.302585
1	0	0	0
2	0.301030	1	0.693147
3	0.477121	1.584963	1.098612
4	0.602060	2	1.386294
5	0.698970	2.321928	1.609438
6	0.778151	2.584963	1.791759
7	0.845098	2.807355	1.945910
8	0.903090	3	2.079442
9	0.954243	3.169925	2.197225
10	1	3.321928	2.302585
20	1.301030	4.321928	2.995732
30	1.477121	4.906891	3.401197
40	1.602060	5.321928	3.688879
50	1.698970	5.643856	3.912023
60	1.778151	5.906991	4.094345
70	1.845098	6.129283	4.248495
80	1.903090	6.321928	4.382027
90	1.954243	6.491853	4.499810
100	2	6.643856	4.605170
200	2.301030	7.643856	5.298317
300	2.477121	8.228819	5.703782
400	2.602060	8.643856	5.991465
500	2.698970	8.965784	6.214608
600	2.778151	9.228819	6.396930
700	2.845098	9.451211	6.551080
800	2.903090	9.643856	6.684612
900	2.954243	9.813781	6.802395
1000	3	9.965784	6.907755
10000	4	13.287712	9.210340

 

లోగరిథం కాలిక్యులేటర్

 

---

ఇది కూడ చూడు

• లోగరిథం నియమాలు
• లోగరిథం బేస్ యొక్క మార్పు
• సున్నా యొక్క లోగరిథం
• ఒకటి యొక్క లోగరిథం
• అనంతం యొక్క లోగరిథం
• ప్రతికూల సంఖ్య యొక్క లోగరిథం
• లోగరిథం కాలిక్యులేటర్
• లోగరిథం గ్రాఫ్
• లోగరిథం పట్టిక
• సహజ లాగరిథం కాలిక్యులేటర్
• సహజ లాగరిథం - ln x
• e స్థిరాంకం
• డెసిబెల్ (డిబి)