ఆర్కోస్ (x) ఫంక్షన్
ఆర్కోస్ (x), కాస్ -1 (x), విలోమ కొసైన్ ఫంక్షన్.
ఆర్కోస్ నిర్వచనం
X యొక్క ఆర్కోసిన్ -1≤x≤1 ఉన్నప్పుడు x యొక్క విలోమ కొసైన్ ఫంక్షన్ గా నిర్వచించబడింది .
Y యొక్క కొసైన్ x కి సమానంగా ఉన్నప్పుడు:
cos y = x
X యొక్క ఆర్కోసిన్ x యొక్క విలోమ కొసైన్ ఫంక్షన్కు సమానం, ఇది y కి సమానం:
arccos x = cos -1 x = y
(ఇక్కడ కాస్ -1 ఎక్స్ అంటే విలోమ కొసైన్ మరియు -1 యొక్క శక్తికి కొసైన్ అని అర్ధం కాదు).
ఉదాహరణ
arccos 1 = cos -1 1 = 0 rad = 0 °
ఆర్కోస్ యొక్క గ్రాఫ్
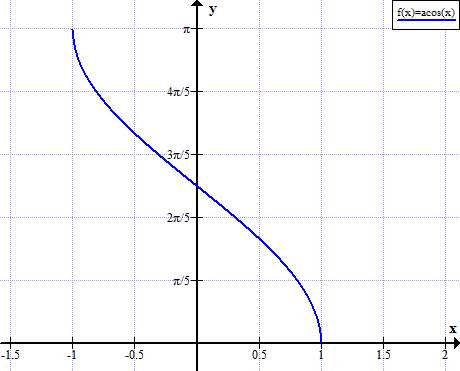
ఆర్కోస్ నియమాలు
| నియమం పేరు | నియమం |
|---|---|
| ఆర్కోసిన్ యొక్క కొసైన్ | cos (arccos x ) = x |
| కొసైన్ యొక్క ఆర్కోసిన్ | k ∈ℤ ( k పూర్ణాంకం) ఉన్నప్పుడు arccos (cos x ) = x + 2 k |
| ప్రతికూల వాదన యొక్క ఆర్కోస్ | arccos (- x ) = π - arccos x = 180 ° - arccos x |
| పరిపూరకరమైన కోణాలు | arccos x = π / 2 - arcsin x = 90 ° - arcsin x |
| ఆర్కోస్ మొత్తం | arccos ( α ) + arccos ( β ) = arccos ( αβ - √ (1- α 2 ) (1- β 2 ) ) |
| ఆర్కోస్ తేడా | arccos ( α ) - arccos ( β ) = arccos ( αβ + √ (1- α 2 ) (1- β 2 ) ) |
| X యొక్క పాపం యొక్క ఆర్కోస్ | arccos (sin x ) = - x - (2 k +0.5) |
| ఆర్కోసిన్ సైన్ | |
| ఆర్కోసిన్ యొక్క టాంజెంట్ |  |
| ఆర్కోసిన్ యొక్క ఉత్పన్నం | 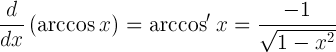 |
| ఆర్కోసిన్ యొక్క నిరవధిక సమగ్ర | |
ఆర్కోస్ టేబుల్
| x | ఆర్కోస్ (x) (రాడ్) |
ఆర్కోస్ (x) (°) |
|---|---|---|
| -1 | π | 180 ° |
| -√ 3 /2 | 5π / 6 | 150 ° |
| -√ 2 /2 | 3π / 4 | 135 ° |
| -1/2 | 2π / 3 | 120 ° |
| 0 | / 2 | 90 ° |
| 1/2 | / 3 | 60 ° |
| √ 2 /2 | / 4 | 45 ° |
| √ 3 /2 | / 6 | 30 ° |
| 1 | 0 | 0 ° |
ఇది కూడ చూడు
- కొసైన్ ఫంక్షన్
- ఆర్క్సిన్ ఫంక్షన్
- ఆర్క్టాన్ఫంక్షన్
- ఆర్కోస్ కాలిక్యులేటర్
- రేడియన్స్ టు డిగ్రీల కన్వర్టర్
- 0 యొక్క ఆర్కోస్
- 1 యొక్క ఆర్కోస్
- 2 యొక్క ఆర్కోస్
- 3 యొక్క ఆర్కోస్
- కాస్ యొక్క ఆర్కోస్
- పాపం యొక్క ఆర్కోస్
- ఆర్కోస్ ఉత్పన్నం
- ఆర్కోస్ గ్రాఫ్
- ఆర్కోస్ యొక్క కాస్
- ఆర్కోస్ యొక్క పాపం
- టాన్ ఆఫ్ ఆర్కోస్