ฟังก์ชัน Arccos (x)

arccos (x), cos -1 (x) ผกผันโคไซน์ฟังก์ชั่น

นิยาม Arccos

arccosine ของ x ถูกกำหนดให้เป็นฟังก์ชันโคไซน์ผกผันของ x เมื่อ-1≤x≤1

เมื่อโคไซน์ของ y เท่ากับ x:

cos y = x

จากนั้น arccosine ของ x จะเท่ากับฟังก์ชันโคไซน์ผกผันของ x ซึ่งเท่ากับ y:

arccos x = cos -1 x = y

(ในที่นี้ cos -1 x หมายถึงโคไซน์ผกผันและไม่ได้หมายถึงโคไซน์ที่มีกำลัง -1)

ตัวอย่าง

arccos 1 = cos -1 1 = 0 rad = 0 °

กราฟของ arccos

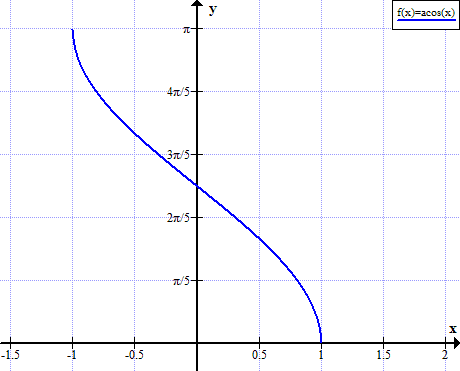
กฎ Arccos

ชื่อกฎ กฎ
โคไซน์ของอาร์คโคซีน cos (arccos x ) = x
Arccosine ของโคไซน์ arccos (cos x ) = x + 2 k πเมื่อk ∈ℤ ( kเป็นจำนวนเต็ม)
Arccos ของอาร์กิวเมนต์เชิงลบ arccos (- x ) = π - arccos x = 180 ° - arccos x
มุมเสริม arccos x = π / 2 - arcsin x = 90 ° - arcsin x
ผลรวม Arccos arccos ( α ) + arccos ( β ) =
   arccos ( αβ - √ (1- α 2 ) (1- β 2 ) )
ความแตกต่างของ Arccos arccos ( α ) - arccos ( β ) =
   arccos ( αβ + √ (1- α 2 ) (1- β 2 ) )
Arccos ของบาปของ x arccos (บาปx ) = - x - (2 k +0.5) π
ไซน์ของ arccosine
แทนเจนต์ของ arccosine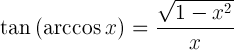
อนุพันธ์ของ arccosine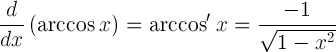
อินทิกรัลไม่ จำกัด ของอาร์คโคซีน

ตาราง Arccos

x arccos (x)

(rad)

 arccos (x)

(°)
-1 π 180 °
-√ 3 /2 5π / 6 150 °
-√ 2 /2 3π / 4 135 °
-1/2 2π / 3 120 °
0 π / 2 90 °
1/2 π / 3 60 °
√ 2 /2 π / 4 45 °
√ 3 /2 π / 6 30 °
1 0 0 °

 

ดูสิ่งนี้ด้วย

ตรีโกณมิติ
ตารางอย่างรวดเร็ว