Arccos (x) işlevi
Arccos (x), cos -1 (x), ters kosinüs fonksiyonu.
Arccos tanımı
X'in arkkosinüsü, -1≤x≤1 olduğunda x'in ters kosinüs fonksiyonu olarak tanımlanır .
Y'nin kosinüsü x'e eşit olduğunda:
çünkü y = x
O zaman, x'in arkkosinüsü, x'in ters kosinüs fonksiyonuna eşittir, bu da y'ye eşittir:
arccos x = cos -1 x = y
(Burada cos -1 x, ters kosinüs anlamına gelir ve kosinüsü -1'in kuvvetine göre ifade etmez).
Misal
arccos 1 = cos -1 1 = 0 rad = 0 °
Arccos grafiği
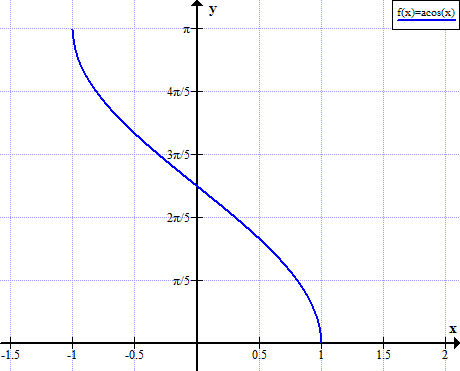
Arccos kuralları
| Kural adı | Kural |
|---|---|
| Arkkosinüsün kosinüsü | cos (arccos x ) = x |
| Kosinüs arkkosinüsü | arccos (cos x ) = x + 2 k π, k ∈ℤ ( k tam sayıdır) |
| Negatif argümanın arkcoları | arccos (- x ) = π - arccos x = 180 ° - arccos x |
| Tamamlayıcı açılar | arccos x = π / 2 - arcsin x = 90 ° - arcsin x |
| Arccos toplamı | arccos ( α ) + arccos ( β ) = arccos ( αβ - √ (1- α 2 ) (1- β 2 ) ) |
| Arccos farkı | arccos ( α ) - arccos ( β ) = arccos ( αβ + √ (1- α 2 ) (1- β 2 ) ) |
| X'in günahlarının arkcoları | arccos (günah x ) = - x - (2 k +0,5) π |
| Arkkosinüs sinüsü | |
| Arkkosin tanjantı |  |
| Arkkosin türevi | 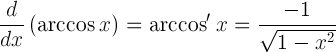 |
| Arkkosinin belirsiz integrali | |
Arccos tablosu
| x | arccos (x) (rad) |
arccos (x) (°) |
|---|---|---|
| -1 | π | 180 ° |
| -√ 3 /2 | 5π / 6 | 150 ° |
| -√ 2 /2 | 3π / 4 | 135 ° |
| -1/2 | 2π / 3 | 120 ° |
| 0 | π / 2 | 90 ° |
| 1/2 | π / 3 | 60 ° |
| √ 2 /2 | π / 4 | 45 ° |
| √ 3 /2 | π / 6 | 30 ° |
| 1 | 0 | 0 ° |
Ayrıca bakınız
- Kosinüs işlevi
- Arcsine işlevi
- Arktanfonksiyon
- Arccos hesap makinesi
- Radyan - Derece dönüştürücü
- Arccos of 0
- 1 Arccos
- Arccos of 2
- Arccos of 3
- Arccos of cos
- Günahın arkcoları
- Arccos türevi
- Arccos grafiği
- Arccos nedeniyle
- Arccos'un günahı
- Arccos Tan