Функція Arccos (x)
Arccos (x), cos -1 (x), обернена косинусова функція.
Визначення дуги
Аркосинус x визначається як обернена косинусова функція x, коли -1≤x≤1.
Коли косинус y дорівнює x:
cos y = x
Тоді аркосинус x дорівнює оберненій косинусній функції x, яка дорівнює y:
arccos x = cos -1 x = y
(Тут cos -1 x означає зворотний косинус і не означає косинус до ступеня -1).
Приклад
arccos 1 = cos -1 1 = 0 рад = 0 °
Графік дуг
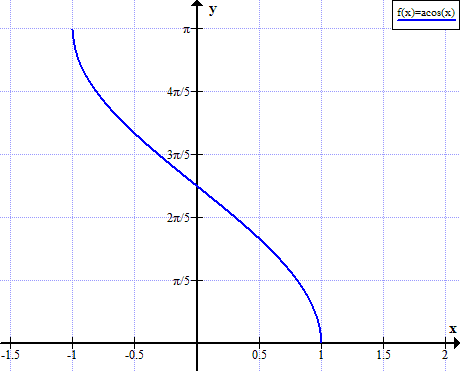
Правила Arccos
| Назва правила | Правило |
|---|---|
| Косинус аркозинуса | cos (arccos x ) = x |
| Аркосинус косинуса | arccos (cos x ) = x + 2 k π, коли k ∈ℤ ( k - ціле число) |
| Дуги негативних аргументів | arccos (- x ) = π - arccos x = 180 ° - arccos x |
| Додаткові кути | arccos x = π / 2 - arcsin x = 90 ° - arcsin x |
| Сума арккос | arccos ( α ) + arccos ( β ) = arccos ( αβ - √ (1- α 2 ) (1- β 2 ) ) |
| Різниця дуг | arccos ( α ) - arccos ( β ) = arccos ( αβ + √ (1- α 2 ) (1- β 2 ) ) |
| Arccos гріха x | arccos (sin x ) = - x - (2 k +0,5) π |
| Синус арккосинуса | |
| Тангенс аркозину | 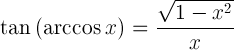 |
| Похідне аркозину | 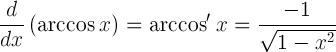 |
| Невизначений інтеграл аркозину | |
Стіл Arccos
| х | arccos (x) (рад) |
arccos (x) (°) |
|---|---|---|
| -1 | π | 180 ° |
| -√ 3 /2 | 5π / 6 | 150 ° |
| -√ 2 /2 | 3π / 4 | 135 ° |
| -1/2 | 2π / 3 | 120 ° |
| 0 | π / 2 | 90 ° |
| 1/2 | π / 3 | 60 ° |
| √ 2 /2 | π / 4 | 45 ° |
| √ 3 /2 | π / 6 | 30 ° |
| 1 | 0 | 0 ° |
Дивіться також
- Функція косинуса
- Функція Arcsine
- Функція арктана
- Калькулятор Arccos
- Перетворювач радіанів в градуси
- Дуги 0
- Арккос 1
- Дуги 2
- Арккос 3
- Arccos з cos
- Арккос гріха
- Похідна дуги
- Граф Arccos
- Кос дуг
- Гріх arccos
- Засмага дуги