反正弦函數
arcsin(x),sin -1(x),反正弦函數。
Arcsin定義
x的反正弦定義為逆正弦x的函數時-1≤x≤1。
當y的正弦等於x時:
罪y = x
那麼x的反正弦等於x的反正弦函數,它等於y:
反正弦x = sin -1 x = y
例
反正弦1 =正弦-1 1 =π/ 2弧度= 90°
圖的反正弦
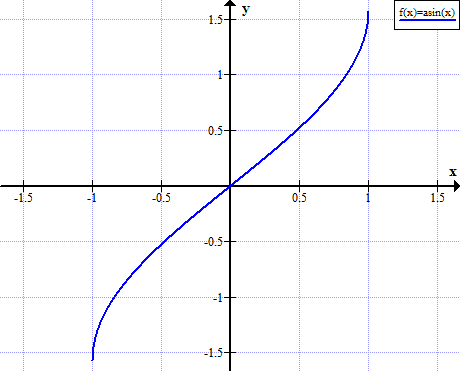
阿辛規則
| 規則名稱 | 規則 |
|---|---|
| 反正弦 | sin(arcsin x)= x |
| 正弦反正弦 | 反正弦(SIN X)= X 2 ķ π,當ķ ∈ℤ(ķ是整數) |
| 否定論的阿克辛 | arcsin(-x)=-arcsin x |
| 互補角 | arcsin x =π/ 2-arccos x = 90°-arccos x |
| 反正弦和 | 反正弦α +反正弦(β)=反正弦(α√ (1- β 2) + β√ (1- α 2)) |
| 反正弦差 | 反正弦α -反正弦(β)=反正弦(α√ (1- β 2) - β√ (1- α 2)) |
| 反正弦餘弦 | |
| 反正切線 | |
| 反正弦的導數 | 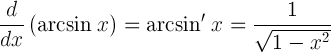 |
| 反正弦的不定積分 |
Arcsin表
| x | 反正弦(x) (rad) |
反正弦(x) (°) |
|---|---|---|
| -1 | -π/ 2 | -90° |
| -√ 3 /2 | -π/ 3 | -60° |
| -√ 2 /2 | -π/ 4 | -45° |
| -1/2 | -π/ 6 | -30° |
| 0 | 0 | 0度 |
| 1/2 | π/ 6 | 30° |
| √ 2 /2 | π/ 4 | 45° |
| √ 3 /2 | π/ 3 | 60度 |
| 1 | π/ 2 | 90° |
也可以看看
- 正弦函數
- 反餘弦函數
- Arctan功能
- Arcsin計算器
- 度到弧度轉換器
- 0的反正弦
- 1的反正弦
- 無限的反正弦
- 反正弦圖
- Arcsin衍生物
- Arcsin積分
- 反正弦的罪
- 反正弦餘弦
- Tan of arcsin