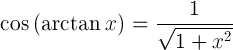反正切函數
Arctan(x),tan -1(x),反正切函數。
Arctan定義
x的反正切定義為當x為實(x∈ℝ)時x的反正切函數。
當y的切線等於x時:
黃褐色ÿ = X
那麼x的反正切等於x的反正切函數,它等於y:
arctan x = tan -1 x = y
例
arctan 1 = tan -1 1 =π/ 4 rad = 45°
圖的arctan
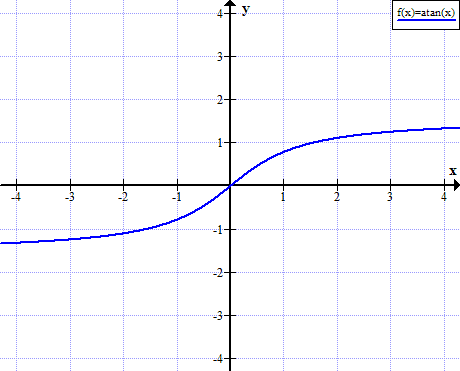
Arctan規則
| 規則名稱 | 規則 |
|---|---|
| 反正切 | tan(arctan x)= x |
| 否定論的奧秘 | arctan(-x)=-arctan x |
| 奧秘總和 | 反正切α +反正切β =反正切[(α + β)/(1- αβ)] |
| Arctan差異 | 反正切α -反正切β =反正切[(αβ)/(1 + αβ)] |
| 反正切正弦 | |
| 反正切餘弦 | |
| 相互論證 | 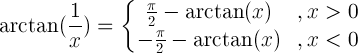 |
| 來自arcsin的arctan | |
| arctan的衍生物 | |
| arctan的不定積分 | |
Arctan表
| x | arctan(x) (rad) |
arctan(x) (°) |
|---|---|---|
| -∞ | -π/ 2 | -90° |
| -3 | -1.2490 | -71.565° |
| -2 | -1.1071 | -63.435° |
| -√ 3 | -π/ 3 | -60° |
| -1 | -π/ 4 | -45° |
| -1 /√ 3 | -π/ 6 | -30° |
| -0.5 | -0.4636 | -26.565° |
| 0 | 0 | 0度 |
| 0.5 | 0.4636 | 26.565° |
| 1 /√ 3 | π/ 6 | 30° |
| 1 | π/ 4 | 45° |
| √ 3 | π/ 3 | 60度 |
| 2 | 1.1071 | 63.435° |
| 3 | 1.2490 | 71.565° |
| ∞ | π/ 2 | 90° |