e konstanta
Konstanta ili Eulerov broj je matematička konstanta. E konstanta je stvaran i iracionalan broj.
e = 2,718281828459 ...
Definicija e
E konstanta je definirana kao ograničenje:
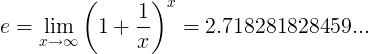
Alternativne definicije
E konstanta je definirana kao ograničenje:
![]()
E konstanta je definirana kao beskonačni niz:
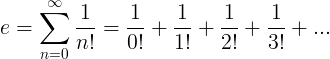
Svojstva e
Uzajamno od e
Uzajamnost e je granica:
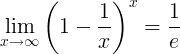
Izvedeni iz e
Izvod eksponencijalne funkcije je eksponencijalna funkcija:
( e x ) '= e x
Izvod funkcije prirodnog logaritma je recipročna funkcija:
(log e x ) '= (ln x )' = 1 / x
Integrali e
Neodređeni integral eksponencijalne funkcije e x je eksponencijalna funkcija e x .
∫ e x dx = e x + c
Neodređeni integral funkcije prirodnog logaritma log e x je:
∫ log e x dx = ∫ ln x dx = x ln x - x + c
Definitivni integral od 1 do e uzajamne funkcije 1 / x je 1:
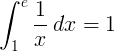
Baza e logaritam
Prirodni logaritam broja x definiran je kao osnovni e logaritam x:
ln x = log e x
Eksponencijalna funkcija
Eksponencijalna funkcija definirana je kao:
f ( x ) = exp ( x ) = e x
Eulerova formula
Kompleksni broj e iθ ima identitet:
e iθ = cos ( θ ) + i sin ( θ )
i je zamišljena jedinica (kvadratni korijen od -1).
θ je bilo koji stvarni broj.
Vidi također
- Kako e 2.71828183?
- Logaritamska pravila
- Prirodni logaritam
- Pravila eksponenata
- Normalna distribucija
- Konstanta Pi
- e konstanta - wikipedia