Nulti broj (0)
Definicija nultog broja
Nula je broj koji se koristi u matematici da ne bi opisao veličinu ili nulu.
Kada su 2 jabuke na stolu i uzmemo 2 jabuke, možemo reći da na stolu nema nula jabuka.
Nulti broj nije pozitivan broj i nije negativan broj.
Nula je također znamenka rezerviranog mjesta u drugim brojevima (npr. 40,103, 170).
Je li nula broj?
Nula je broj. To nije pozitivan ni negativan broj.
Nulta znamenka
Nulta znamenka koristi se kao rezervirano mjesto pri pisanju brojeva.
Na primjer:
204 = 2 × 100 + 0 × 10 + 4 × 1
Povijest nultog broja
Tko je izumio nulti broj?
Suvremeni simbol 0 izumljen je u Indiji u 6. stoljeću, a kasnije su ga koristili Perzijanci i Arapi, a kasnije i Europa.
Simbol nule
Nulti broj označen je simbolom 0 .
Arapski brojevni sustav koristi simbol ٠.
Svojstva nultog broja
x predstavlja bilo koji broj.
| Operacija | Pravilo | Primjer |
|---|---|---|
Dodatak |
x + 0 = x |
3 + 0 = 3 |
Oduzimanje |
x - 0 = x |
3 - 0 = 3 |
Množenje |
x × 0 = 0 |
5 × 0 = 0 |
Podjela |
0 ÷ x = 0 , kada je x ≠ 0 |
0 ÷ 5 = 0 |
| x ÷ 0 nije definiran |
5 ÷ 0 nije definirano |
|
Pojačavanje |
0 x = 0 |
0 5 = 0 |
| x 0 = 1 |
5 0 = 1 |
|
Korijen |
√ 0 = 0 |
|
Logaritam |
log b (0) nije definiran |
|
| |
||
Faktorijel |
0! = 1 |
|
Sinus |
sin 0º = 0 |
|
Kosinus |
cos 0º = 1 |
|
Tangens |
preplanuli 0º = 0 |
|
Izvedena |
0 '= 0 |
|
Sastavni |
∫ 0 d x = 0 + C |
|
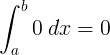 |
Nulti dodatak
Zbrajanje broja plus nula jednako je broju:
x + 0 = x
Na primjer:
5 + 0 = 5
Nula oduzimanje
Oduzimanje broja minus nula jednako je broju:
x - 0 = x
Na primjer:
5 - 0 = 5
Množenje s nulom
Množenje broja pomnoženo s nulom jednako je nuli:
x × 0 = 0
Na primjer:
5 × 0 = 0
Broj podijeljen s nulom
Podjela broja s nulom nije definirana:
x ÷ 0 nije definiran
Na primjer:
5 ÷ 0 nije definirano
Nula podijeljena s brojem
Podjela nule brojem je nula:
0 ÷ x = 0
Na primjer:
0 ÷ 5 = 0
Broj na nulu snage
Moć broja podignutog nulom je jedna:
x 0 = 1
Na primjer:
5 0 = 1
Logaritam nule
Logaritam baze n nula je nedefiniran:
log b (0) nije definiran
Ne postoji broj s kojim možemo povisiti bazu b da bismo dobili nulu.
Samo je granica osnovnog b logaritma x, kada x konvergira nuli, minus beskonačnost:
![]()
Skupine koje sadrže nulu
Nula je element prirodnih brojeva, cjelobrojnih brojeva, realnih brojeva i skupova složenih brojeva:
| Postavi | Postavite oznaku članstva |
|---|---|
| Prirodni brojevi (ne negativni) | 0 ∈ ℕ 0 |
| Cijeli brojevi | 0 ∈ ℤ |
| Stvarni brojevi | 0 ∈ ℝ |
| Složeni brojevi | 0 ∈ ℂ |
| Racionalni brojevi | 0 ∈ ℚ |
Je li nula paran ili neparan broj?
Skup parnih brojeva je:
{..., -10, -8, -6, -4, -2, 0, 2, 4, 6, 8, 10, ...}
Skup neparnih brojeva je:
{..., -9, -7, -5, -3, -1, 1, 3, 5, 7, 9, ...}
Nula je cijeli broj višestruki od 2:
0 × 2 = 0
Nula je član skupa parnih brojeva:
0 ∈ {2 k , k ∈ℤ}
Dakle, nula je paran, a ne neparan broj.
Je li nula prirodni broj?
Postoje dvije definicije za skup prirodnih brojeva.
Skup negativnih cijelih brojeva:
ℕ 0 = {0,1,2,3,4,5,6,7,8, ...}
Skup pozitivnih cijelih brojeva:
ℕ 1 = {1,2,3,4,5,6,7,8, ...}
Nula je član skupa negativnih cijelih brojeva:
0 ∈ ℕ 0
Nula nije član skupa pozitivnih cijelih brojeva:
0 ∉ ℕ 1
Je li nula cijeli broj?
Postoje tri definicije za cijele brojeve:
Skup cjelobrojnih brojeva:
ℤ = {0,1,2,3,4,5,6,7,8, ...}
Skup negativnih cijelih brojeva:
ℕ 0 = {0,1,2,3,4,5,6,7,8, ...}
Skup pozitivnih cijelih brojeva:
ℕ 1 = {1,2,3,4,5,6,7,8, ...}
Nula je član skupa cijelih brojeva i skupa negativnih cijelih brojeva:
0 ∈ ℤ
0 ∈ ℕ 0
Nula nije član skupa pozitivnih cijelih brojeva:
0 ∉ ℕ 1
Je li nula cjelobrojni broj?
Skup cjelobrojnih brojeva:
ℤ = {0,1,2,3,4,5,6,7,8, ...}
Nula je član skupa cjelobrojnih brojeva:
0 ∈ ℤ
Dakle, nula je cijeli broj.
Je li nula racionalan broj?
Racionalni broj je broj koji se može izraziti kao količnik dvaju cjelobrojnih brojeva:
ℚ = { n / m ; n , m ∈ℤ}
Nula se može zapisati kao količnik dvaju cijelih brojeva.
Na primjer:
0 = 0/3
Dakle, nula je racionalan broj.
Je li nula pozitivan broj?
Pozitivan broj definira se kao broj veći od nule:
x / 0
Na primjer:
5/ 0
Budući da nula nije veća od nule, to nije pozitivan broj.
Je li nula prost broj?
Broj 0 nije prost broj.
Nula nije pozitivan broj i ima beskonačan broj djelitelja.
Najmanji prosti broj je 2.