ಲಾಗರಿಥಮ್ ನಿಯಮಗಳು

ಬೇಸ್ ಬಿ ಕ್ರಮಾವಳಿ ಸಂಖ್ಯೆ ಒಂದು ಘಾತ ನಾವು ಸಂಗ್ರಹಿಸಲು ಅಗತ್ಯವಿರುವ ಮೂಲ ಸಂಖ್ಯೆ ಪಡೆಯಲು ಸಲುವಾಗಿ.

ಲಾಗರಿಥಮ್ ವ್ಯಾಖ್ಯಾನ

B ಯನ್ನು y ನ ಶಕ್ತಿಗೆ ಏರಿಸಿದಾಗ ಸಮಾನ x:

b y = x

ನಂತರ x ನ ಮೂಲ b ಲಾಗರಿಥಮ್ y ಗೆ ಸಮಾನವಾಗಿರುತ್ತದೆ:

ಲಾಗ್ ಬಿ ( ಎಕ್ಸ್ ) = ವೈ

ಉದಾಹರಣೆಗೆ ಯಾವಾಗ:

2 4 = 16

ನಂತರ

ಲಾಗ್ 2 (16) = 4

ಲೋಗರಿಥಮ್ ಘಾತೀಯ ಕ್ರಿಯೆಯ ವಿಲೋಮ ಕ್ರಿಯೆಯಾಗಿ

ಲಾಗರಿಥಮಿಕ್ ಕ್ರಿಯೆ,

y = ಲಾಗ್ b ( x )

ಘಾತೀಯ ಕ್ರಿಯೆಯ ವಿಲೋಮ ಕ್ರಿಯೆ,

x = b ವೈ

ಆದ್ದರಿಂದ ನಾವು x (x/ 0) ನ ಲಾಗರಿಥಮ್‌ನ ಘಾತೀಯ ಕಾರ್ಯವನ್ನು ಲೆಕ್ಕ ಹಾಕಿದರೆ,

f ( f -1 ( x )) = b ಲಾಗ್ b ( x ) = x

ಅಥವಾ ನಾವು x ನ ಘಾತೀಯ ಕ್ರಿಯೆಯ ಲಾಗರಿಥಮ್ ಅನ್ನು ಲೆಕ್ಕ ಹಾಕಿದರೆ,

f -1 ( f ( x )) = ಲಾಗ್ b ( b x ) = x

ನೈಸರ್ಗಿಕ ಲಾಗರಿಥಮ್ (ಎಲ್ಎನ್)

ನೈಸರ್ಗಿಕ ಲಾಗರಿಥಮ್ ಬೇಸ್ಗೆ ಲಾಗರಿಥಮ್ ಆಗಿದೆ:

ln ( x ) = ಲಾಗ್ ಇ ( x )

ಯಾವಾಗ ಇ ನಿರಂತರ ಸಂಖ್ಯೆ:

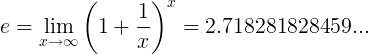
e = \ lim_ {x \ rightarrow \ infty} \ left (1+ \ frac {1} {x} \ right) ^ x = 2.718281828459 ...

ಅಥವಾ

e = \ lim_ {x \ ಬಲಗಡೆ 0} \ ಎಡ (1+ \ ಬಲ x) ^ \ frac {1} {x}

 

ನೋಡಿ: ನೈಸರ್ಗಿಕ ಲಾಗರಿಥಮ್

ವಿಲೋಮ ಲಾಗರಿಥಮ್ ಲೆಕ್ಕಾಚಾರ

ವಿಲೋಮ ಲಾಗರಿಥಮ್ (ಅಥವಾ ವಿರೋಧಿ ಲಾಗರಿಥಮ್) ಅನ್ನು ಲಾಗರಿಥಮ್ y ಗೆ ಬೇಸ್ b ಅನ್ನು ಹೆಚ್ಚಿಸುವ ಮೂಲಕ ಲೆಕ್ಕಹಾಕಲಾಗುತ್ತದೆ:

x = ಲಾಗ್ -1 ( ವೈ ) = ಬಿ ವೈ

ಲಾಗರಿಥಮಿಕ್ ಕ್ರಿಯೆ

ಲಾಗರಿಥಮಿಕ್ ಕಾರ್ಯವು ಇದರ ಮೂಲ ರೂಪವನ್ನು ಹೊಂದಿದೆ:

f ( x ) = ಲಾಗ್ b ( x )

ಲಾಗರಿಥಮ್ ನಿಯಮಗಳು

ನಿಯಮದ ಹೆಸರು ನಿಯಮ
ಲಾಗರಿಥಮ್ ಉತ್ಪನ್ನ ನಿಯಮ
 log b ( x y ) = log b ( x ) + log b ( y )
ಲಾಗರಿಥಮ್ ಅಂಶ ನಿಯಮ
 log b ( x / y ) = log b ( x ) - log b ( y )
ಲಾಗರಿಥಮ್ ವಿದ್ಯುತ್ ನಿಯಮ
 log b ( x y ) = y log b ( x )
ಲಾಗರಿಥಮ್ ಬೇಸ್ ಸ್ವಿಚ್ ನಿಯಮ
 ಲಾಗ್ ಬಿ ( ಸಿ ) = 1 / ಲಾಗ್ ಸಿ ( ಬಿ )
ಲಾಗರಿಥಮ್ ಮೂಲ ಬದಲಾವಣೆಯ ನಿಯಮ
 ಲಾಗ್ ಬಿ ( ಎಕ್ಸ್ ) = ಲಾಗ್ ಸಿ ( ಎಕ್ಸ್ ) / ಲಾಗ್ ಸಿ ( ಬಿ )
ಲಾಗರಿಥಮ್ನ ವ್ಯುತ್ಪನ್ನ
 f ( x ) = ಲಾಗ್ b ( x ) ⇒ f ' ( x ) = 1 / ( x ln ( b ))
ಲಾಗರಿಥಮ್‌ನ ಸಮಗ್ರ
 ∫ ಲಾಗ್ ಬಿ ( ಎಕ್ಸ್ ) ಡಿಎಕ್ಸ್ = ಎಕ್ಸ್ ∙ (ಲಾಗ್ ಬಿ ( ಎಕ್ಸ್ ) - 1 / ಎಲ್ಎನ್ ( ಬಿ ) ) + ಸಿ
ನಕಾರಾತ್ಮಕ ಸಂಖ್ಯೆಯ ಲಾಗರಿಥಮ್
 x ≤ 0 ಆಗಿರುವಾಗ ಲಾಗ್ b ( x ) ಅನ್ನು ವ್ಯಾಖ್ಯಾನಿಸಲಾಗುವುದಿಲ್ಲ
0 ರ ಲಾಗರಿಥಮ್
 ಲಾಗ್ ಬಿ (0) ಅನ್ನು ವಿವರಿಸಲಾಗಿಲ್ಲ
\ lim_ {x \ ರಿಂದ 0 ^ +} \ textup {log} _b (x) = - \ infty
1 ರ ಲಾಗರಿಥಮ್
 ಲಾಗ್ ಬಿ (1) = 0
ಬೇಸ್ನ ಲಾಗರಿಥಮ್
 ಲಾಗ್ ಬಿ ( ಬಿ ) = 1
ಅನಂತತೆಯ ಲಾಗರಿಥಮ್
 ಲಿಮ್ ಲಾಗ್ ಬಿ ( ಕ್ಷ ) = ∞, ಆಗ ಕ್ಷ → ∞

ನೋಡಿ: ಲಾಗರಿಥಮ್ ನಿಯಮಗಳು

 

ಲಾಗರಿಥಮ್ ಉತ್ಪನ್ನ ನಿಯಮ

X ಮತ್ತು y ನ ಗುಣಾಕಾರದ ಲಾಗರಿಥಮ್ x ನ ಲಾಗರಿಥಮ್ ಮತ್ತು y ನ ಲಾಗರಿಥಮ್ನ ಮೊತ್ತವಾಗಿದೆ.

log b ( x y ) = log b ( x ) + log b ( y )

ಉದಾಹರಣೆಗೆ:

ಲಾಗ್ 10 (3 ∙ 7) = ಲಾಗ್ 10 (3) + ಲಾಗ್ 10 (7)

ಲಾಗರಿಥಮ್ ಅಂಶ ನಿಯಮ

X ಮತ್ತು y ನ ವಿಭಜನೆಯ ಲಾಗರಿಥಮ್ x ನ ಲಾಗರಿಥಮ್ ಮತ್ತು y ನ ಲಾಗರಿಥಮ್ನ ವ್ಯತ್ಯಾಸವಾಗಿದೆ.

log b ( x / y ) = log b ( x ) - log b ( y )

ಉದಾಹರಣೆಗೆ:

ಲಾಗ್ 10 (3 / 7) = ಲಾಗ್ 10 (3) - ಲಾಗ್ 10 (7)

ಲಾಗರಿಥಮ್ ವಿದ್ಯುತ್ ನಿಯಮ

Y ನ ಶಕ್ತಿಗೆ ಬೆಳೆದ x ನ ಲಾಗರಿಥಮ್ x ನ ಲಾಗರಿಥಮ್‌ನ y ಪಟ್ಟು.

log b ( x y ) = y log b ( x )

ಉದಾಹರಣೆಗೆ:

ಲಾಗ್ 10 (2 8 ) = 8 ∙ ಲಾಗ್ 10 (2)

ಲಾಗರಿಥಮ್ ಬೇಸ್ ಸ್ವಿಚ್ ನಿಯಮ

ಸಿ ಯ ಮೂಲ ಬಿ ಲಾಗರಿಥಮ್ ಅನ್ನು 1 ರ ಮೂಲ ಸಿ ಲಾಗರಿಥಮ್ನಿಂದ ಭಾಗಿಸಲಾಗಿದೆ.

ಲಾಗ್ ಬಿ ( ಸಿ ) = 1 / ಲಾಗ್ ಸಿ ( ಬಿ )

ಉದಾಹರಣೆಗೆ:

ಲಾಗ್ 2 (8) = 1 / ಲಾಗ್ 8 (2)

ಲಾಗರಿಥಮ್ ಮೂಲ ಬದಲಾವಣೆಯ ನಿಯಮ

X ನ ಬೇಸ್ ಬಿ ಲಾಗರಿಥಮ್ x ನ ಬೇಸ್ ಸಿ ಲಾಗರಿಥಮ್ ಅನ್ನು b ನ ಬೇಸ್ ಸಿ ಲಾಗರಿಥಮ್ನಿಂದ ಭಾಗಿಸಲಾಗಿದೆ.

ಲಾಗ್ ಬಿ ( ಎಕ್ಸ್ ) = ಲಾಗ್ ಸಿ ( ಎಕ್ಸ್ ) / ಲಾಗ್ ಸಿ ( ಬಿ )

ಉದಾಹರಣೆಗೆ, ಕ್ಯಾಲ್ಕುಲೇಟರ್‌ನಲ್ಲಿ ಲಾಗ್ 2 (8) ಅನ್ನು ಲೆಕ್ಕಾಚಾರ ಮಾಡಲು, ನಾವು ಬೇಸ್ ಅನ್ನು 10 ಕ್ಕೆ ಬದಲಾಯಿಸಬೇಕಾಗಿದೆ:

ಲಾಗ್ 2 (8) = ಲಾಗ್ 10 (8) / ಲಾಗ್ 10 (2)

ನೋಡಿ: ಲಾಗ್ ಬೇಸ್ ಚೇಂಜ್ ರೂಲ್

ನಕಾರಾತ್ಮಕ ಸಂಖ್ಯೆಯ ಲಾಗರಿಥಮ್

X ನಕಾರಾತ್ಮಕವಾಗಿದ್ದಾಗ ಅಥವಾ ಶೂನ್ಯಕ್ಕೆ ಸಮನಾದಾಗ x <= 0 ಅನ್ನು ವ್ಯಾಖ್ಯಾನಿಸದಿದ್ದಾಗ x ನ ಮೂಲ ಬಿ ನೈಜ ಲಾಗರಿಥಮ್:

x ≤ 0 ಆಗಿರುವಾಗ ಲಾಗ್ b ( x ) ಅನ್ನು ವ್ಯಾಖ್ಯಾನಿಸಲಾಗುವುದಿಲ್ಲ

ನೋಡಿ: ನಕಾರಾತ್ಮಕ ಸಂಖ್ಯೆಯ ಲಾಗ್

0 ರ ಲಾಗರಿಥಮ್

ಶೂನ್ಯದ ಮೂಲ ಬಿ ಲಾಗರಿಥಮ್ ಅನ್ನು ವಿವರಿಸಲಾಗಿಲ್ಲ:

ಲಾಗ್ ಬಿ (0) ಅನ್ನು ವಿವರಿಸಲಾಗಿಲ್ಲ

X ಶೂನ್ಯವನ್ನು ಸಮೀಪಿಸಿದಾಗ x ನ ಮೂಲ b ಲಾಗರಿಥಮ್‌ನ ಮಿತಿ ಮೈನಸ್ ಅನಂತ:

\ lim_ {x \ ರಿಂದ 0 ^ +} \ textup {log} _b (x) = - \ infty

ನೋಡಿ: ಶೂನ್ಯದ ಲಾಗ್

1 ರ ಲಾಗರಿಥಮ್

ಒಂದರ ಮೂಲ ಬಿ ಲಾಗರಿಥಮ್ ಶೂನ್ಯ:

ಲಾಗ್ ಬಿ (1) = 0

ಉದಾಹರಣೆಗೆ, ಒಂದರ ಎರಡು ಲಾಗರಿಥಮ್ ಶೂನ್ಯವಾಗಿರುತ್ತದೆ:

ಲಾಗ್ 2 (1) = 0

ನೋಡಿ: ಒಂದರ ಲಾಗ್

ಅನಂತತೆಯ ಲಾಗರಿಥಮ್

X ಅನಂತವನ್ನು ಸಮೀಪಿಸಿದಾಗ x ನ ಮೂಲ b ಲಾಗರಿಥಮ್‌ನ ಮಿತಿ ಅನಂತಕ್ಕೆ ಸಮಾನವಾಗಿರುತ್ತದೆ:

ಲಿಮ್ ಲಾಗ್ ಬಿ ( ಕ್ಷ ) = ∞, ಆಗ ಕ್ಷ → ∞

ನೋಡಿ: ಅನಂತತೆಯ ದಾಖಲೆ

ಬೇಸ್ನ ಲಾಗರಿಥಮ್

B ಯ ಮೂಲ b ಲಾಗರಿಥಮ್ ಒಂದಾಗಿದೆ:

ಲಾಗ್ ಬಿ ( ಬಿ ) = 1

ಉದಾಹರಣೆಗೆ, ಎರಡರ ಮೂಲ ಎರಡು ಲಾಗರಿಥಮ್ ಒಂದು:

ಲಾಗ್ 2 (2) = 1

ಲೋಗರಿಥಮ್ ಉತ್ಪನ್ನ

ಯಾವಾಗ

f ( x ) = ಲಾಗ್ b ( x )

ನಂತರ f (x) ನ ಉತ್ಪನ್ನ:

f ' ( x ) = 1 / ( x ln ( b ))

ನೋಡಿ: ಲಾಗ್ ಉತ್ಪನ್ನ

ಲಾಗರಿಥಮ್ ಅವಿಭಾಜ್ಯ

X ನ ಲಾಗರಿಥಮ್‌ನ ಅವಿಭಾಜ್ಯ:

∫ ಲಾಗ್ ಬಿ ( ಎಕ್ಸ್ ) ಡಿಎಕ್ಸ್ = ಎಕ್ಸ್ ∙ (ಲಾಗ್ ಬಿ ( ಎಕ್ಸ್ ) - 1 / ಎಲ್ಎನ್ ( ಬಿ ) ) + ಸಿ

ಉದಾಹರಣೆಗೆ:

∫ ಲಾಗ್ 2 ( x ) ಡಿಎಕ್ಸ್ = ಎಕ್ಸ್ ∙ (ಲಾಗ್ 2 ( ಎಕ್ಸ್ ) - 1 / ಎಲ್ಎನ್ (2) ) + ಸಿ

ಲಾಗರಿಥಮ್ ಅಂದಾಜು

ಲಾಗ್ 2 ( x ) ≈ n + ( x / 2 n - 1),

ಸಂಕೀರ್ಣ ಲಾಗರಿಥಮ್

ಸಂಕೀರ್ಣ ಸಂಖ್ಯೆ z ಗಾಗಿ:

z = re iθ = x + iy

ಸಂಕೀರ್ಣ ಲಾಗರಿಥಮ್ ಇರುತ್ತದೆ (n = ...- 2, -1,0,1,2, ...):

ಲಾಗ್ z = ln ( r ) + i ( θ + 2nπ ) = ln ( x ( x 2 + y 2 )) + i · arctan ( y / x ))

ಲಾಗರಿಥಮ್ ಸಮಸ್ಯೆಗಳು ಮತ್ತು ಉತ್ತರಗಳು

ಸಮಸ್ಯೆ # 1

ಇದಕ್ಕಾಗಿ x ಅನ್ನು ಹುಡುಕಿ

ಲಾಗ್ 2 ( x ) + ಲಾಗ್ 2 ( x -3) = 2

ಪರಿಹಾರ:

ಉತ್ಪನ್ನ ನಿಯಮವನ್ನು ಬಳಸುವುದು:

ಲಾಗ್ 2 ( x ( x -3)) = 2

ಲಾಗರಿಥಮ್ ವ್ಯಾಖ್ಯಾನಕ್ಕೆ ಅನುಗುಣವಾಗಿ ಲಾಗರಿಥಮ್ ಫಾರ್ಮ್ ಅನ್ನು ಬದಲಾಯಿಸುವುದು:

x ( x -3) = 2 2

ಅಥವಾ

x 2 -3 x -4 = 0

ಚತುರ್ಭುಜ ಸಮೀಕರಣವನ್ನು ಪರಿಹರಿಸುವುದು:

x 1,2 = [3 ± √ (9 + 16)] / 2 = [3 ± 5] / 2 = 4, -1

ಲಾಗರಿಥಮ್ ಅನ್ನು negative ಣಾತ್ಮಕ ಸಂಖ್ಯೆಗಳಿಗೆ ವ್ಯಾಖ್ಯಾನಿಸಲಾಗಿಲ್ಲವಾದ್ದರಿಂದ, ಉತ್ತರ ಹೀಗಿದೆ:

x = 4

ಸಮಸ್ಯೆ # 2

ಇದಕ್ಕಾಗಿ x ಅನ್ನು ಹುಡುಕಿ

ಲಾಗ್ 3 ( x +2) - ಲಾಗ್ 3 ( x ) = 2

ಪರಿಹಾರ:

ಅಂಶ ನಿಯಮವನ್ನು ಬಳಸುವುದು:

ಲಾಗ್ 3 (( x +2) / x ) = 2

ಲಾಗರಿಥಮ್ ವ್ಯಾಖ್ಯಾನಕ್ಕೆ ಅನುಗುಣವಾಗಿ ಲಾಗರಿಥಮ್ ಫಾರ್ಮ್ ಅನ್ನು ಬದಲಾಯಿಸುವುದು:

( x +2) / x = 3 2

ಅಥವಾ

x +2 = 9 x

ಅಥವಾ

8 x = 2

ಅಥವಾ

x = 0.25

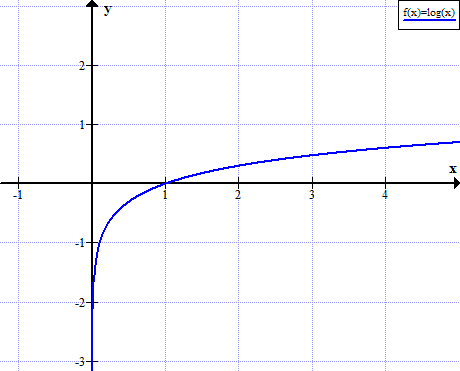
ಲಾಗ್ (x) ನ ಗ್ರಾಫ್

x ನ ನೈಜ ಧನಾತ್ಮಕವಲ್ಲದ ಮೌಲ್ಯಗಳಿಗೆ ಲಾಗ್ (x) ಅನ್ನು ವ್ಯಾಖ್ಯಾನಿಸಲಾಗಿಲ್ಲ:

ಲಾಗರಿಥಮ್ಸ್ ಟೇಬಲ್

x ಲಾಗ್ 10 x ಲಾಗ್ 2 x ಲಾಗ್ ಇ x
0 ಸ್ಪಷ್ಟೀಕರಿಸದ ಸ್ಪಷ್ಟೀಕರಿಸದ ಸ್ಪಷ್ಟೀಕರಿಸದ
0 + - - -
0.0001 -4 -13.287712 -9.210340
0.001 -3 -9.965784 -6.907755
0.01 -2 -6.643856 -4.605170
0.1 -1 -3.321928 -2.302585
1 0 0 0
2 0.301030 1 0.693147
3 0.477121 1.584963 1.098612
4 0.602060 2 1.386294
5 0.698970 2.321928 1.609438
6 0.778151 2.584963 1.791759
7 0.845098 2.807355 1.945910
8 0.903090 3 2.079442
9 0.954243 3.169925 2.197225
10 1 3.321928 2.302585
20 1.301030 4.321928 2.995732
30 1.477121 4.906891 3.401197
40 1.602060 5.321928 3.688879
50 1.698970 5.643856 3.912023
60 1.778151 5.906991 4.094345
70 1.845098 6.129283 4.248495
80 1.903090 6.321928 4.382027
90 1.954243 6.491853 4.499810
100 2 6.643856 4.605170
200 2.301030 7.643856 5.298317
300 2.477121 8.228819 5.703782
400 2.602060 8.643856 5.991465
500 2.698970 8.965784 6.214608
600 2.778151 9.228819 6.396930
700 2.845098 9.451211 6.551080
800 2.903090 9.643856 6.684612
900 2.954243 9.813781 6.802395
1000 3 9.965784 6.907755
10000 4 13.287712 9.210340

 

ಲಾಗರಿಥಮ್ ಕ್ಯಾಲ್ಕುಲೇಟರ್

 

ಸಹ ನೋಡಿ

ಅಲ್ಜೀಬ್ರಾ
ರಾಪಿಡ್ ಟೇಬಲ್‌ಗಳು