对数规则
数字的底数b对数是我们为了获得数字而需要提高底数的指数。
对数定义
当b提高到y的幂等于x时:
b y = x
然后,x的基数b对数等于y:
log b(x)= y
例如,当:
2 4 = 16
然后
对数2(16)= 4
对数为指数函数的反函数
对数函数
y = log b(x)
是指数函数的反函数,
x = b y
因此,如果我们计算x(x/ 0)的对数的指数函数,
f(f -1(x))= b log b (x) = x
或者,如果我们计算x的指数函数的对数,
f -1(f(x))= log b(b x)= x
自然对数(ln)
自然对数是以e为底的对数:
ln(x)= log e(x)
当e常数是数字时:
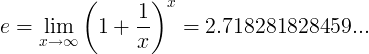
或
![]()
请参阅:自然对数
反对数计算
通过将底数b提高到对数y来计算反对数(或反对数):
x = log -1(y)= b y
对数函数
对数函数的基本形式为:
f(x)=对数b(x)
对数规则
| 规则名称 | 规则 |
|---|---|
对数乘积规则 |
log b(x∙y)= log b(x)+ log b(y) |
对数商法则 |
日志b(X / Y)=日志b(X)-日志b(Ý) |
对数幂规则 |
log b(x y)= y∙ log b(x) |
对数基数切换规则 |
log b(c)= 1 / log c(b) |
对数基数更改规则 |
log b(x)= log c(x)/ log c(b) |
对数导数 |
f(x)=对数b(x) ⇒f '(x)= 1 /(x ln(b)) |
对数积分 |
∫ 日志b(X)DX = X∙(日志b(X) - 1 / LN(b) )+ C ^ |
负数的对数 |
日志b(X)是未定义当 X ≤0 |
对数0 |
日志b(0)未定义 |
1的对数 |
log b(1)= 0 |
底数的对数 |
log b(b)= 1 |
无穷大的对数 |
LIM日志b(X)= ∞,当X →∞ |
另请:对数规则
对数乘积规则
x和y的对数是x和y的对数之和。
log b(x∙y)= log b(x)+ log b(y)
例如:
日志10(3 ∙ 7)=日志10(3)+日志10(7)
对数商法则
x和y的对数是x和y的对数之差。
日志b(X / Y)=日志b(X)-日志b(Ý)
例如:
日志10(3 / 7)=日志10(3)-日志10(7)
对数幂规则
x的对数提高到y的幂是y乘以x的对数。
log b(x y)= y∙ log b(x)
例如:
日志10(2 8)= 8 ∙日志10(2)
对数基数切换规则
c的底b对数为1除以b的底c对数。
log b(c)= 1 / log c(b)
例如:
log 2(8)= 1 / log 8(2)
对数基数更改规则
x的底b对数是x的底c对数除以b的底c对数。
log b(x)= log c(x)/ log c(b)
例如,为了在计算器中计算对数2(8),我们需要将底数更改为10:
日志2(8)=日志10(8)/日志10(2)
请参阅:日志基准更改规则
负数的对数
当x <= 0时,当x为负或等于零时,x的基数b实对数不确定:
日志b(X)是未定义当 X ≤0
请参阅:负数日志
对数0
未定义以b为底的对数:
日志b(0)未定义
x接近零时,x的基b对数的极限为负无穷大:
![]()
请参阅:零对数
1的对数
1的底b对数为零:
log b(1)= 0
例如,以1为底的两个对数为零:
对数2(1)= 0
另请:日志一
无穷大的对数
x接近无穷大时,x的基b对数的极限等于无穷大:
当x →∞时lim log b(x)= ∞
请参阅:无限对数
底数的对数
b的底b对数为1:
log b(b)= 1
例如,以2为底的对数为1:
对数2(2)= 1
对数导数
什么时候
f(x)=对数b(x)
然后f(x)的导数:
f'(x)= 1 /(x ln(b))
另请:对数导数
对数积分
x的对数的积分:
∫ 日志b(X)DX = X∙(日志b(X) - 1 / LN(b) )+ C ^
例如:
∫ 日志2(X)DX = X∙(日志2(X) - 1 / LN(2) )+ C ^
对数近似
日志2(X)≈ Ñ +(X / 2 Ñ - 1),
复数对数
对于复数z:
z = reiθ = x + iy
复数对数为(n = ...- 2,-1,0,1,2,...):
对数z = ln(r)+ i(θ+2nπ)= ln(√(x 2 + y 2))+ i ·arctan(y / x))
对数问题与解答
问题1
查找x
log 2(x)+ log 2(x -3)= 2
解:
使用产品规则:
对数2(x∙(x -3))= 2
根据对数定义更改对数形式:
x∙(x -3)= 2 2
或
x 2 -3 x -4 = 0
求解二次方程:
x 1,2 = [3±√(9 + 16)] / 2 = [3±5] / 2 = 4,-1
由于没有为负数定义对数,因此答案是:
x = 4
问题二
查找x
log 3(x +2)-log 3(x)= 2
解:
使用商规则:
对数3((x +2)/ x)= 2
根据对数定义更改对数形式:
(x +2)/ x = 3 2
或
x +2 = 9 x
或
8 x = 2
或
x = 0.25
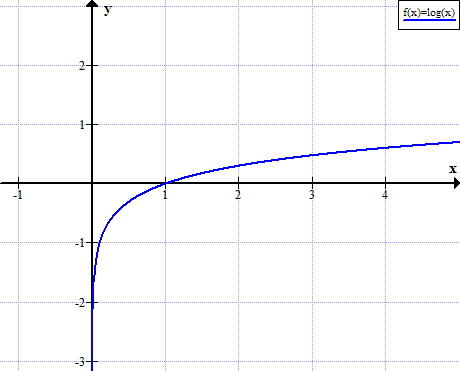
对数图(x)
没有为x的实数非正值定义log(x):
对数表
| x | 记录10 x | 日志2 x | 登录Ë X |
|---|---|---|---|
| 0 | 未定义 | 未定义 | 未定义 |
| 0 + | -∞ | -∞ | -∞ |
| 0.0001 | -4 | -13.287712 | -9.210340 |
| 0.001 | -3 | -9.965784 | -6.907755 |
| 0.01 | -2 | -6.643856 | -4.605170 |
| 0.1 | -1 | -3.321928 | -2.302585 |
| 1 | 0 | 0 | 0 |
| 2 | 0.301030 | 1 | 0.693147 |
| 3 | 0.477121 | 1.584963 | 1.098612 |
| 4 | 0.602060 | 2 | 1.386294 |
| 5 | 0.698970 | 2.321928 | 1.609438 |
| 6 | 0.778151 | 2.584963 | 1.791759 |
| 7 | 0.845098 | 2.807355 | 1.945910 |
| 8 | 0.903090 | 3 | 2.079442 |
| 9 | 0.954243 | 3.169925 | 2.197225 |
| 10 | 1 | 3.321928 | 2.302585 |
| 20 | 1.301030 | 4.321928 | 2.995732 |
| 30 | 1.477121 | 4.906891 | 3.401197 |
| 40 | 1.602060 | 5.321928 | 3.688879 |
| 50 | 1.698970 | 5.643856 | 3.912023 |
| 60 | 1.778151 | 5.906991 | 4.094345 |
| 70 | 1.845098 | 6.129283 | 4.248495 |
| 80 | 1.903090 | 6.321928 | 4.382027 |
| 90 | 1.954243 | 6.491853 | 4.499810 |
| 100 | 2 | 6.643856 | 4.605170 |
| 200 | 2.301030 | 7.643856 | 5.298317 |
| 300 | 2.477121 | 8.228819 | 5.703782 |
| 400 | 2.602060 | 8.643856 | 5.991465 |
| 500 | 2.698970 | 8.965784 | 6.214608 |
| 600 | 2.778151 | 9.228819 | 6.396930 |
| 700 | 2.845098 | 9.451211 | 6.551080 |
| 800 | 2.903090 | 9.643856 | 6.684612 |
| 900 | 2.954243 | 9.813781 | 6.802395 |
| 1000 | 3 | 9.965784 | 6.907755 |
| 10000 | 4 | 13.287712 | 9.210340 |