指數規則
指數規則,指數定律和例子。
什麼是指數
以n為底的a等於a的乘積,n倍:
a n = a × a × ... × a
n次
a是基數,n是指數。
例子
3 1 = 3
3 2 = 3×3 = 9
3 3 = 3×3×3 = 27
3 4 = 3×3×3×3 = 81
3 5 = 3×3×3×3×3 = 243
指數規則和屬性
| 規則名稱 | 規則 | 例 |
|---|---|---|
| 產品規則 | 一個Ñ ⋅一米=一個n + m個 | 2 3 ⋅2 4 = 2 3 + 4 = 128 |
| 一個Ñ ⋅ b Ñ =(一個⋅ b)ñ | 3 2 ⋅4 2 =(3⋅4)2 = 144 | |
| 商規則 | a n / a m = a n - m | 2 5 /2 3 = 2 5-3 = 4 |
| a n / b n =(a / b)n | 4 3 /2 3 =(4/2)3 = 8 | |
| 功率規則 | (b Ñ)米= b n⋅m | (2 3)2 = 23⋅2 = 64 |
| b n m = b( n m) | 2 3 2 = 2(3 2)= 512 | |
| 米√( b Ñ)= b ñ /米 | 2 √(2 6)= 2 6/2 = 8 | |
| b 1 / Ñ = Ñ √ b | 8 1/3 = 3 √ 8 = 2 | |
| 負指數 | b -n = 1 / b n | 2 -3 = 1/2 3 = 0.125 |
| 零規則 | b 0 = 1 | 5 0 = 1 |
| 0 n = 0,n / 0時 | 0 5 = 0 | |
| 一個規則 | b 1 = b | 5 1 = 5 |
| 1 n = 1 | 1 5 = 1 | |
| 減一法則 | 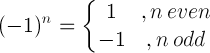 |
(-1)5 = -1 |
| 導數規則 | (X Ñ)' = ñ ⋅ X Ñ -1 | (X 3)' =3⋅ X 3-1 |
| 積分規則 | ∫ X Ñ DX = X Ñ 1 /(Ñ 1)+ C ^ | ∫ X 2 DX = X 2 + 1 /(2 + 1)+ C ^ |
指數產品規則
具有相同基數的產品規則
一個Ñ ⋅一米=一個n + m個
例:
2 3 ⋅2 4 = 2 3 + 4 = 2 7 =2⋅2⋅2⋅2⋅2⋅2⋅2= 128
具有相同指數的乘積規則
一個Ñ ⋅ b Ñ =(一個⋅ b)ñ
例:
3 2 ⋅4 2 =(3⋅4)2 = 12 2 =12⋅12= 144
請參閱:多重指數
指數商規則
具有相同底數的商數規則
a n / a m = a n - m
例:
2 5 /2 3 = 2 5-3 = 2 2 =2⋅2= 4
具有相同指數的商法則
a n / b n =(a / b)n
例:
4 3 /2 3 =(4/2)3 = 2 3 =2⋅2⋅2= 8
另請:指數除法
指數冪規則
功率規則I
(一Ñ)米=一個n⋅m
例:
(2 3)2 = 23⋅2 = 2 6 =2⋅2⋅2⋅2⋅2⋅2= 64
權力規則二
a n m = a ( n m)
例:
2 3 2 = 2(3 2)= 2(3⋅3)= 2 9 =2⋅2⋅2⋅2⋅2⋅2⋅2⋅2⋅2= 512
部首的權力統治
米√(一Ñ)=一個ñ /米
例:
2 √(2 6)= 2 6/2 = 2 3 =2⋅2⋅2= 8
負指數規則
b -n = 1 / b n
例:
2 -3 = 1/2 3 = 1 /(2⋅2⋅2)= 1/8 = 0.125
請參閱:負指數